Mikko Mikkolaa*, Thomas Tingelöfb and Jari K. Ihonenb
a Helsinki University of Technology, Department of Applied Physics, Advanced Energy Systems,
P.O. Box 5100, 02015 TKK, Finland, b VTT, Technical Research Centre of Finland P.O. Box 1000
FIN-02044, Finland
[*] Corresponding author: tel. + 358-9-4513209, fax. + 358-9-4513195, e-mail
[email protected]
Abstract
A general purpose 3D finite element method model has been developed for the estimation of the compression pressure distribution in fuel cell stacks. The model can be used for the optimisation of any type of fuel cell structure at any temperature. The model was validated with pressure sensitive film measurements using PEFC stack components that had low rigidity and were highly deformable.
keywords: stack, clamping pressure, pressure distribution, modelling, FEM
1. Introduction
Uniform compression pressure distribution over the active area and gaskets of the fuel cell stack is essential to its performance and life-time [1] as it has a major impact on the properties of the gas diffusion layer (GDL) and contact resistances [2-10], affecting both current and temperature distributions. The compression pressure is uneven both under the ribs in the flow fields [1,11-13], as well as over the whole membrane electrode assembly (MEA) and gaskets [14-16].
For the low temperature fuel cells the pressure distribution can be measured experimentally near operating temperature using pressure sensitive films. For high temperature fuel cells this is not possible, due to a limited operating temperature range of the pressure sensitive films. Therefore, the compression pressure distribution within a high temperature fuel cell stack must be modelled, which creates a need for an experimentally validated modelling tool. With a high quality modelling tool, optimal end plate structures and clamping schemes of both high and low temperature fuel cells can be readily designed.
In the past a few attempts have been made to simulate the compression pressure within a polymer electrolyte fuel cell (PEFC) using FEM computer models [14-15,22]. Lee et al. modelled the pressure distribution inside a small unit cell and validated their model with experiments [14]. However, there was up to a 60% difference between model predictions and measurement results, but quantitatively, the trends in results were similar. Liu et al. presented a method to optimise the assembly pressure and clamping bolt locations to achieve more uniform pressure distribution in a unit cell [15]. Their work did not contain experimental validation. Karvonen et al. used a FEM model to investigate pressure distribution in a multicell stack, and compared various end plate structures and materials and clamping force schemes [2]. Their validation process did not include numerical comparison, but qualitatively the results were in agreement. The developed models have shown the importance of correct end plate design and clamping pressure application, but none of them can reliably predict the compression pressure distribution inside a cell or a stack.
The purpose of this work was to develop and validate a widely applicable model that can accurately predict pressure distributions within any type of fuel cell at any temperature. A 3D FEM computer model was developed and validated through experiments with pressure sensitive films using in3 house PEFC stack with highly deformable components. Results from validation experiments proved the applicability of the model.
2. Description of the model
2.1 Theory
The equation which is solved in the model is where D is the elasticity matrix and u is the deformation vector consisting of deformations u, v, and w in x-, y- and z-directions, respectively:
From the solution, stress and strain components can be calculated. In this work, we are mostly interested in the perpendicular stress on stack components. For example, stress in the z-direction can be written as
where E is Young’s modulus and v Poisson’s ratio. Theoretical background can be found in more detail in e.g. [17] or any structural mechanics text book, for example [18].
2.2 Model details
The fuel cell model geometry used in this model is based on an existing fuel cell stack design on which experiments could readily be carried out. Stack structure was simplified for computational and experimental validation purposes by omitting bipolar plates, porous transport layers and gaskets and including only end plates, flexible equalization layers (EQL), current collectors and bipolar plate substitute. The resulting structure is artificial but still corresponds closely to the situation in the first and last cells in the real stacks, where the compression pressure distribution is usually the most uneven. Further into the stack, the flexibility of cell components makes the pressure distribution more even.
The model is comprised of five separate domains, which were the 40 mm thick end plate, 5 mm thick equalization layer, 10 mm current collector, 1 mm bipolar plate substitute and gas line connector substitutes. The EQL was optional, and was not used in all the modelled cases. The model geometry is shown in Figure 1. The geometry of each component is identical to the real geometry of the actual stack components except the bipolar plate substitute, which is identical in xy dimensions, but thinner and does not contain flow channels.

Figure 1: Left: Model geometry and symmetry planes 1) End plate 2) Equalization layer 3) Current collector 4) Bipolar plate substitute 5) Gas line connector substitute. Right: Areas used for clamping force boundary conditions.
Due to symmetry, the model implements only one eighth of the stack. Symmetry conditions were applied onto all internal section boundaries. A symmetry boundary condition was also applied onto the bottom of the bipolar plate substitute, corresponding to the experimental scenario where the stack is assembled with a thin layer of PTFE in place of bipolar plates. In the model, clamping forces were applied on a washer-shaped area around each bolt hole. The inner and outer diameters were 9 and 16 mm, respectively, giving an area of 1.37 *-4 m2. All other boundaries were free. 5 Young’s modulus
and Poisson’s ratio were needed for each component to model their deformation under stress. Manufacturer supplied and literature data was used whenever available. Table 1 contains a list of modelled components, their dimensions, materials and material parameters, and data sources.
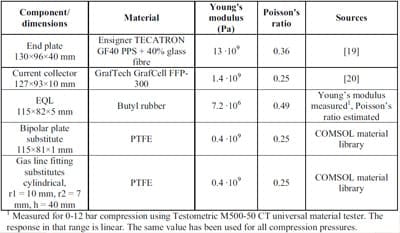
Table 1: Material parameters used in the model
The model was implemented using Comsol Multiphysics® 3.4, a commercial FEM solver, running on a computer with a dual core AMD Opteron 265 processor, 16 GB of RAM, and GNU/Linux OpenSUSE 10.3 64-bit operating system. The theory of the FEM can for instance be found in the textbook by Zienkiewicz et al. [21].
3. Experimental
3.1 Pressure distribution measurement apparatus
For the validation measurements, a new metal-free end plate structure was developed for a previously designed in-house stack. The structure included relatively soft end plates made of fibre glass reinforce polyphenylene sulphide (TECATRON GF 40, Ensigner Ltd.), expanded natural graphite current collectors (GRAFCELL® FFP-300, GrafTech Inc.) and butyl rubber (polyisobutadiene) flexible equalisation layers (EQLs). The EQLs between end plates and current collectors deform and thereby transfer pressure from the high pressure regions to the low pressure regions. The developed new end plate structure is metal free. The motivation for the development of the metal-free structure comes from the fact that cations, especially Fe2+ and Cu2+, released from any other metal part of the system can act as catalysts for radical formation from H2O2 and also decrease the conductivity of the membrane [22-25]. Therefore, to maximise polymer fuel cell life6 time it is desirable to eliminate all metallic components in parts of the fuel cell system that are in contact with humidified reactant gas flows.
The experimental set-up is shown in Figure 2. Between the current collectors a bipolar plate substitute (two 0.5 mm thick PTFE sheets) was added to reduce the disturbing effect of the current collector roughness on the pressure distribution measurements and to avoid discolouration of the pressure sensitive films by the current collectors. Pressure sensitive films (Pressurex® Super Low Pressure LLW) were placed within the bipolar plate substitute, see Figure 2. The compression pressure was exerted by a stack of disc springs (Mubea Tellerfedern GmbH) around each clamping bolt.

Figure 2: Left: Stack overview. Right: Stack quarter section view along symmetry planes
A set of calibration measurements, in the range of 3 to 28 bar, were performed to obtain a relation between the colour intensity in the pressure sensitive film and applied pressure. The resulting calibration curve was used in data processing to convert the colour pattern on the pressure sensitive film to numeric pressure distribution data. The applicable pressure range was found to be 4 to 25 bar.
In all experimental work reported here was carried out under controlled ambient conditions. Air temperature and relative humidity were maintained at 23°C and 50%, respectively. Impact time for all pressure sensitive film measurements was 2 hours. All measurements were performed twice.
3.2 Test procedure for validation of the computer model
Five test cases, see Table 2, were compiled for model validation. Pressure distribution between the bipolar plate substitutes was both modelled and experimentally measured for all cases. The effect of equalization layer was investigated with three test cases: no equalization layer, basic equalization layer and modified equalization layer. The basic EQL is solid, except for the holes required for clamping bolts and gas channels. The modified, but non-optimised EQL contains additional holes, which modify the overall rigidity in the vicinity of the holes, see Figure 3. Furthermore, Figure 3 shows the location of 6 by 4 grid of 15 mm by 15 mm squares, into which the active area was divided. This grid was used in the model validation process.
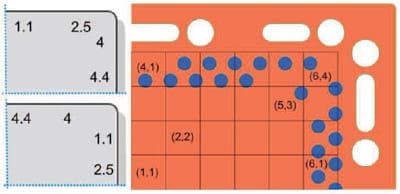
Figure 3: Left: Clamping force cases. Top: Case 4, bottom: Case 5. Right: Equalization layer. The basic EQL does not have the perforations marked with darker colour. Below, the locations of grid squares are given using the coordinate system shown in this figure.
Three test cases were also used for clamping force distribution. Case 3 is a base case in which 3 kN force was applied to all clamping bolts. In cases 4 and 5, the majority of the force was applied around the bolts on the short and long edges of the stack, respectively. Clamping forces and their locations can be seen in Figure 3. In all three cases the total force applied onto one quarter of the end plate is 12 kN. This corresponds to an average pressure of 12.5 bar on the EQL and bipolar plate substitute, which both have an area of ca. 96 cm2.
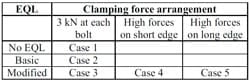
Table 2: Test cases for model validation
The results from the model and the measured data were analyzed in the following way. Resulting pressure maps were scanned at 300 DPI to digital format and processed using Matlab®. Since the system is symmetric the measured data was averaged over one quarter of the active area in order to get a larger statistical selection. To reduce noise, the data from the scans was further averaged over squares so that the final images had ca. 104 data points
The colouration of the pressure maps were converted into surface pressures using the obtained calibration curve. Since data measured above the saturation limit of the pressure sensitive film cannot be considered reliable all data indicating pressures higher than the saturation limit were set to 25 Bar. To analyse the results, the compression pressure over the active area was integrated over the grid squares shown in Figure 3, and resulting forces were compared between the measurement and modelling results.
4 Results and discussion 4.1 Modelling results
Modelled clamping pressure distributions over the active area are presented in Figure 4 for different cases in Table 2. Although the pressure distribution was modelled and measured over the whole area of the bipolar plate substitute, only the distribution on the active area is shown in the figures. In case 1 there is no EQL present the system to transfer pressure from high pressure regions to low pressure regions and the compression pressure is applied to the outer edges of the active area, especially the outer corner. In case 2 a solid EQL is applied which compensates for the deformation of the end plate and transfers some pressure from the corners towards the middle of the active area. In case 3 an EQL which is modified for increased deformation distributes the pressure even more evenly over the active area.
The compression pressure distribution caused by applying different forces to the bolts in the stack was studied with modified EQL. Comparing test cases 3-5 it can be seen that the clamping force arrangements have a significant impact on the pressure distribution. In case 5, a significant amount of pressure has been transferred to the middle of the active area due to EQL deformation.
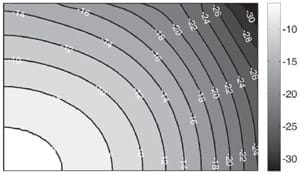
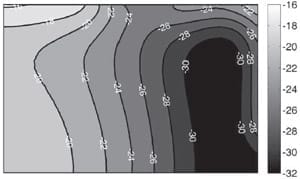
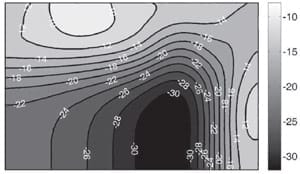
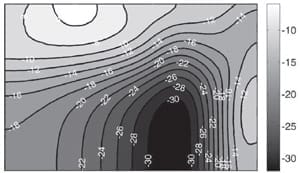
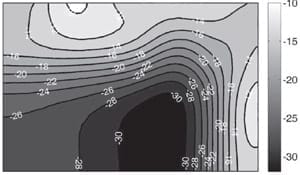
Figures 4 a) to e): Cases 1 to 5, respectively. Modelled pressure distributions on the bottom of the bipolar plate substitute over a 90 by 60 mm rectangle on the active area. The centre of the stack is at the lower left corner of each picture.
4.2 Experimental results
Measured pressure distributions for Cases 1 to 5 are shown in Figure 5. In all cases, the measured pressure distributions show the same trends as the model predictions. However, there are notable quantitative differences in areas where the measured pressure is close to the upper or lower limit of the pressure sensitive film’s range (4 to 25 bar). Below 4 bar, the pressure does not register on the film, and the colouration reaches saturation at 25 bar. Furthermore, data averaging, which was performed to reduce noise, obscures the areas of highest compression. In general, all measured pressure distributions indicate lower pressures than their modelled counterparts.
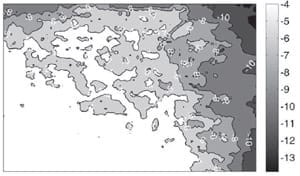
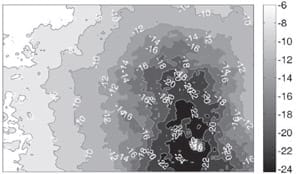
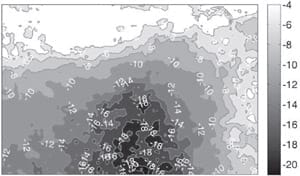

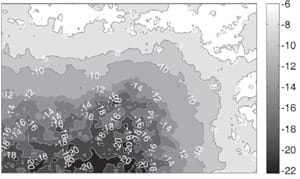
Figures 5 a) to e): Cases 1 to 5, respectively. Measured pressure distributions on the bottom of the bipolar plate substitute over a 90 by 60 mm rectangle on the active area. The centre of the stack is at the lower left corner of each picture. Note the scale in each subpicture.
4.3 Model validation results
Experimental results in Figure 5 show the same trends as model predictions presented in Figure 4. For numerical analysis, the total forces on active areas were determined, see Table 3. Consistently, the model predicts higher compression than the measurements indicate. The most probable cause for this behaviour is the inaccuracy of material parameters used in the model, especially Young’s modulus for the current collector and equalization layer.
Table 3: Total compressive forces on active area for measured and modelled cases, in kN.
The correctness of the shape of the modelled pressure distribution was evaluated using the following procedure. First, the modelling results were limited to the 3 to 25 bar range, i.e. average pressures predicted for each grid square on the active area (see Figure 3) that were above or below the specified range were replaced by the corresponding range limit. Then, for both the modelled and measured results, the pressure on each grid square was scaled by dividing it by the maximum value in that grid. Finally, the error between the measured and modelled was calculated using Equation 4. Error values are presented in Table 4.
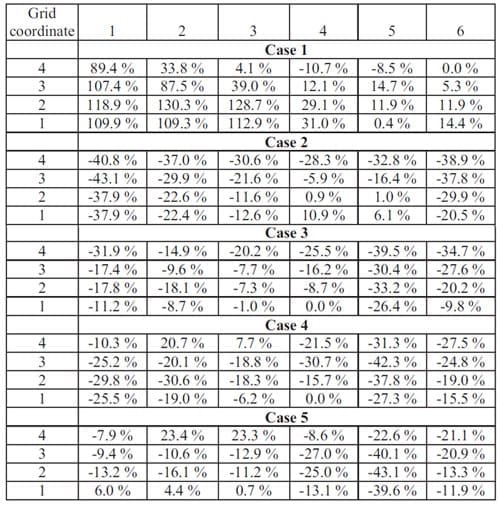
Table 4: The difference between the measured and modelled pressure distributions. The grid coordinates refer to those in Figure 3.
The largest errors in each case are seen where the measured pressure was close to the lower end of the measurable range, but where the measure pressure was between 7 and 20 bar, the error is generally below 30%. This confirms that qualitatively the model predictions are correct. Among the cases, the largest errors occur in Case 1, where close to 80% of the compressive force was exerted outside the active area.
5. Conclusions
An experimentally validated FEM-model which predicts the compression pressure distribution and component deformation within a fuel cell stack has been developed. It shows good qualitative agreement with measured pressure distributions for different equalisation layers, clamping schemes and forces. Quantitatively, the model predicted higher compression pressures than were measured. For a large part, this is due to the limited range of the pressure sensitive film that was used. Here, it was observed that the colour intensity of 10 – 15% of the pixels in the scans of the pressure sensitive films was at saturation limit. In retrospect it is clear that several pressure sensitive films with different pressure ranges should be used in experiments to record a larger portion of the pressure spectra.
Other possible sources of error are the uncertainty in some of the material parameters used in the model, and manufacturing tolerances in the experimental hardware. It has been observed that even small errors in component dimensions can cause notable variations in the pressure distribution [14,18]. The same applies also for small changes in material parameters.
In the future, the validation process will be developed further, and thermal expansion will be included in the model. This, combined with accurate material property data library, will facilitate predicting compression pressure distribution reliably even at elevated temperatures.
Acknowledgements
The financial support of the Finnish Funding Agency for Technology and Innovation (TEKES) is gratefully acknowledged.
Nomenclature
| EQL | Equalization Layer |
| FEM | Finite Element Method |
| GDL | Gas Diffusion Layer |
| MEA | Membrane Electrode Assembly |
| PEFC | Polymer Electrolyte Fuel Cell |
| List of Symbols | |
| σ | stress (N m-2) |
| υ | Poisson’s ratio |
| D | elasticity matrix |
| E | Young’s modulus (Pa) |
| u | deformation vector |
| u,v,w | deformation vector components (m) |
References
- I. Nitta, T. Hottinen, O. Himanen, M. Mikkola, J. Power Sources, 171 (2007) 26-36.
- W. Lee, C. Ho, J.W. Van Zee, M. Murthy, J. Power Sources, 84 (1999) 45-51.
- J. Ihonen, F. Jaouen, G. Lindbergh, G. Sundholm, Electrochimica Acta, 46 (2001) 2899-2911.
- C. Lim, C.Y. Wang, J. Power Sources, 113 (2003) 145-150.
- M. Prasanna, H.Y. Ha, E.A. Cho, S.-A. Hong, I.-H. Oh, J. Power Sources, 131 (2004) 147-154.
- J. Ihonen, M. Mikkola, G. Lindbergh, J. Electrochem. Soc., 151 (2004) A1152-A1161.
- P. Zhou, C.W. Wu, G.J. Ma, J. Power Sources, 159 (2006) 1115-1122.
- J. Ge, A. Higier, H. Liu, J. Power Sources, 159 (2006) 922-927.
- W.R. Chang, J.J. Hwang, F.B. Weng, S.H. Chan, J. Power Sources, 166 (2007) 149-154.
- I. Nitta, O. Himanen, M. Mikkola, Electrochemistry Communications, 10 (2008) 47-51.
- W. Sun, B.A. Peppley, K. Karan, J. Power Sources, 144 (2005) 42-53.
- T. Hottinen, O. Himanen, Electrochem. Comm., 9 (2007) 1047-1052.
- T. Hottinen, O. Himanen, S. Karvonen, I. Nitta, J. Power Sources, 171 (2007) 113-121.
- S. Lee, C. Hsu, C. Huang, J. Power Sources, 145 (2005) 353-361.
- D. Liu, X. Lai, J. Ni, L. Peng, S. Lan, Z. Lin, J. Power Sources, 172 (2007) 760-767.
- X. Wang, Y. Song, B. Zhang, J. Power Sources, 179 (2008) 305-309.
- S. Karvonen, T. Hottinen, J. Ihonen, H. Uusalo, J. Fuel Cell Sci. Technol., 5 (2008) 041009.
- W.C. Young, R.G. Budynas, Roark’s Formulas for Stress and Strain, 7th ed., McGraw-Hill
Professional, New York, USA, 2002, pp. 832. - Ensinger Ltd. TECATRON GF40. Available at:
https://www.ensinger.ltd.uk/docs/datasheets/TECATRON%20GF%2040.pdf. Accessed 2008-07-28. - Grafoil data sheet on GrafTech web site, https://www.graftechaet.com/upload/GHA%20sheet%20properties.pdf. Accessed 2005-10-26.
- O.C. Zienkiewicz, R
.L. Taylor, The Finite Element Method, 5th ed., Elsevier, New York, USA, 2000, pp. 736. - A. Pozio, R.F. Silva, M. De Francesco, L. Giorgi, Electrochimica Acta, 48 (2003) 1543-1549.
- R. Borup, J. Meyers, B. Pivovar, Y.S. Kim, R. Mukundan, N. Garland, D. Myers, M. Wilson,
F. Garzon, D. Wood, P. Zelenay, K. More, K. Stroh, T. Zawodzinski, J. Boncella, J.E. McGrath, M. Inaba, K. Miyatake, M. Hori, K. Ota, Z. Ogumi, S. Miyata, A. Nishikata, Z. Siroma, Y. Uchimoto, K. Yasuda, K.-I. Kimijima, N. Iwashita, Chem. Rev., 107 (2007) 3904-3951. - F.A. de Bruijn, V.A.T. Dam, G.J.M. Janssen, Fuel Cells, 8 (2008) 3-22.
- W. Schmittinger, A. Vahidi, J. Power Sources, 180 (2008) 1-14.


