Mechanical milling for catalyst loading of polymer filters

M.N. Cavalli ^a,*, N. Lilke^b

^a University of North Dakota, Department of Mechanical Engineering, 243 Centennial Drive, Grand Forks, ND 58202-8359, United States
^b University of North Dakota, Department of Electrical Engineering, 243 Centennial Drive, Grand Forks, ND 58202-8155, United States

Abstract

This paper details results of an initial study into the feasibility of using the mechanical milling process as a means of embedding catalyst particles into fabric filters for improved pollution control. The specific combinations of catalysts and filters used in the study to demonstrate the method are currently being explored for use in the energy generation industry to help remove elemental mercury from flue gases. Circular fabric sampleswere placed in a hardened steel milling vial along with a number ofPMMAmilling balls. Catalyst powder and, in some cases, a solvent (water or 70% isopropyl alcohol) were added and the vial milled for 40 min. The fabric samples were then dried and subjected to airflow conditions typical for fabric filters in powerplant baghouses.Weight measurements were used to determine the amount of catalyst retained in the fabric at each stage. Results show that fabric type, number of milling balls used, catalyst powder/fabric mass ratio, particle size and the presence of a solvent can all affect the degree of catalyst loading. The embedded particles adhere well through a number of forward/backpulse cycles simulating airflowconditions in a powerplant baghouse. Modifications are needed to scale such a process to production levels but the current limitations are not insurmountable.

1. Introduction

In Volume II of its 1997, “Mercury Study Report to Congress,” the Environmental Protection Agency (EPA) estimated that coalfired boilers produce over 30% of the total mercury emissions in the United States. The EPA reported that this amounts to more than 40 tons of mercury released into the atmosphere each year from coal-fired boilers alone. Worldwide, Hylander and Goodsite (2006) concluded that coal combustion releases between 750 and 1500 tons of mercury per year into the environment. These mercury emissions are of concern for not only those living in the immediate vicinity of coal-fired plants, but for people around the country and across the globe. In Volume III of the 1997 report, the EPA estimated that more than 75% of the elemental mercury emitted in gaseous form fromeach boiler can travel over 50kmbefore being deposited. Thus there is a high probability that a single mercury emission source can pollute a wide region of the surrounding environment.

Various technologies have been implemented to control the amount of mercury released into the environment during coal combustion. Pavlish et al. (2003) present a summary of the procedures, benefits and drawbacks of available mercury pollution control methods, including sorbent injection, wet scrubbers, fabric filters and coal cleaning. The authors discuss the effectiveness of each method based on variables such as the specific method of combustion, temperatures of the flue gas stream and the chlorine content of the coal. Due to the variety of chemical species present in the flue gases, the complete path of mercury and the kinetics of its transformations are not well understood. Results from Volume VII of the 1997 EPA report, as well as separate work by Brown et al. (2000), have shown that the elemental form of mercury is less readily removed by current technologies, such as wet scrubbing and sorbent injection, than the oxidized species. Brown et al. (2000) did find, however, that fabric filters are able to remove a high degree of elemental mercury in the flue gas stream. Thus a possible method for improving total mercury removal rates from flue gas streams is a treatment sequence involving fabric filters and oxidation of elemental mercury followed by wet scrubbing or sorbent injection.

The integration of properly selected catalyst particles into fabric filters may be an effective method of capturing elemental mercury while also oxidizing the remaining mercury in the flue gas stream. Ness et al. (1995) achieved effective filter coating for a wide variety of catalysts, gas chemistries and filters using a sol–gel technique. Seames et al. (2004) found large variability in the adherence of catalyst particles to different fabric materials using a washcoating process. Glass fiber filters were especially problematic while polymer filters showed much better catalyst retention. A subsequent study by Hrdlicka et al. (2008) found that spray coating and dip coating could provide both effective initial loading and good catalyst retention after simulated service in flue gas streams. Park and Kim (2004) showed that catalyst-coated filters can be used to treat not only flue gases at power plants, but also a variety of pollution streams from industrial processes through the appropriate choice of catalyst chemistry. The use of catalyst-loaded filters has the advantage of possibly reducing overall emissions without significant increases in capital costs. The purpose of the currentwork is to present an alternative method for catalyst loading of fabric filters utilizing the mechanical energy of mechanical milling equipment.

2. Methods

Fig. 1 shows a typical experimental setup in the current work with milling vial, milling spheres and filter fabric.

A circular sample of filter fabric (~40mmdiameter) is placed at the bottom of the hardened steel milling vial. The fabric is milled in one of three conditions, dry, wetted with water, or wetted with 70% isopropyl alcohol. Catalyst powder is placed on the top surface of the fabric layer, milling spheres (9.5mm diameter PMMA) are added and the vial is sealed. The sealed vial is placed horizontally in the milling machine and milled for 40 min. After milling, the fabric sample is dried and weighed to determine the amount of catalyst loading. The sample is then subjected to repeated air pulses to determine how well the catalyst particles are retained.

Fig. 2 shows a schematic representation of the catalyst loading process during milling.

Milling spheres with an initial velocity, V, impact the container wall. Catalyst particles along the line of impact between the spheres and the wall are forced into the open pores of the fabric filter. The depth of the catalyst penetration into the filter depends on variables including particle size, coefficient of friction between the particle and the fabric, kinetic energy of the milling sphere, and size of the open pores in the filter. In the present work, the variables studied were lubrication condition of the fabric, number of milling balls, fabric type, catalyst type and catalyst size. The study variableswere chosen based on preliminary work regarding the most important process parameter
s.

Fig. 1. Milling vial, milling spheres and filter fabric used in catalyst impregnation testing.

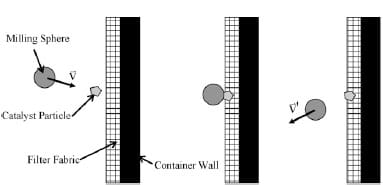
Fig. 2. Schematic of catalyst impregnation via sphere-particle-fabric impact.

Milling was accomplished using a SPEX 8000-M mill (SPEX Certiprep). The milling vial is mounted horizontally and cycled in a three-dimensional motion ‘figure-8’ motion. An accelerometer attached to the exterior of the hardened steel milling vial recorded a milling frequency of approximately 17 Hz, or 1020 milling cycles per minute. The number of PMMA milling spheres in the milling vial was either five or ten.

Two different fabric types were investigated: PT001/P84 and RY805. All fabric was provided by GE (formerly BHA Technologies). PT001/P84 is a non-thermoplastic polyimide. RY805 is a blend of Procon and Torcon, two polyphenlyene sulphide fibers. Both fabrics are currently being used as industrial pollution control filters.

Two catalysts were used in a variety of particles sizes. The first was Al₂O₃ (Sigma–Aldrich) and the second was 5% Pd on Al₂O₃ (Acros Organics). The size ranges tested for Al₂O₃ particles were < 1μm, 10–75μm, 75–150μm. The size ranges tested for Pd on Al2O3 particles were < 75μm, 75–150μm, and < 150μm. Pd on Al2O3 particles were separated using an electromagnetic sieve shaker (Gilson, Inc.). Al₂O₃ particles in the indicated sizes were purchased separately from Sigma–Aldrich.

Catalyst powder was always added in a 1:1 mass ratio with the fabric sample. PT001 samples had a mass of approximately 0.57 g and RY805 samples had amass of approximately 0.5 g. Eachmilling ball had a mass of approximately 0.54 g. When solvent (water or alcohol) was added, the volume was kept constant at 2mL. Each sample was milled for 40 min. Preliminary experiments by the authors showed that this milling timewas sufficient for all samples to reach maximum catalyst loading (some reach maximum loading in as little as 5min depending on the process parameters, most reach it by 20min). Following milling, the samples were heated to 120 ?C for 1 h to dry. Each specimen was then subjected to airflow cycles of 10 s at 275 kPa (forward) and 0.5 s at 550 kPa (backpulse). These airflows and pressures were chosen to simulate those typically seen during forward and backpulse flows in a powerplant baghouse based on a personal conversation with Dr.Michael Mann (2004), a professor of Chemical Engineering at UND and researcher in the area of combustion pollution and pollution control.

3. Results and discussion

Fig. 3 shows several darkfield optical micrographs of both pristine and milled fabrics. Fig. 3a and 3c show pristine PT001 and RY805, respectively. Both fabrics have a three-dimensional structure with comparable fiber thickness. The overall thickness of the PT001 fabric is approximately twice that of RY805 (2.23mmversus 1.05 mm). Fig. 3b shows PT001 that has been milled with 10–75μm Al₂O₃ and water. There is a thin layer of fibers in the foreground which have no catalyst particles attached. Interior fibers appear to have clumps of catalyst particles attached to a large percentage of the fiber surfaces. Fig. 3d shows RY805 that has been milled with nanometer (<1 μm) Al2O3 and 70% isopropyl alcohol. There appears, again, to be a layer of exterior fibers with little attached catalyst. The regions of catalyst in this filter have a much smoother appearance, likely due to the smaller particles sizes being compacted to form each micrometer-sized cluster.

3.1. Effect of process variables on catalyst loading

Table 1 shows the results for initial loading (post-milling) as well as after 5 and 20 backpulse (BP) cycles. The results show that the presence of a solvent can increase the initial catalyst loading as well as the percentage of catalyst retained after several backpulse cycles. With PT001 fabric, the presence of water as a lubricant allowed twice the initial catalyst loading. After 5 backpulse cycles, 94% of the catalyst was retained in the water lubricated sample versus just 18% for the dry sample. Isopropyl alcohol increased the mass fraction of catalyst retained in RY805 by almost 80% over the water-lubricated sample, even after 20 backpulse cycles. Two possible mechanisms for the increased catalyst loading in the presence of either fluid are (1) decrease in coefficient of friction between the catalyst particles in the presence of the lubricant and (2) generation of high internal pressures in the fabric under impact from the milling balls due to near incompressibility of the liquids. Reduced friction would increase the ease with which catalyst particles can be forced into the filters, allowing them to penetrate deeper into the filters and become locked in place once the lubricant is removed. Higher pressures could enlarge openings between fabric fibers and further facilitate particle penetration.

There is a noticeable difference between the initial catalyst loading in the two fabric types for the smallest catalyst particles (<1μm). The PT001 sample had a catalyst mass fraction of 88% following milling while the RY805 sample has a mass fraction of only 51%. Following 20 backpulse cycles, both fabrics retainedmore than 97% of their catalyst loading. The ability to retain small catalyst particles is important from the standpoint that catalyst surface area affects howwell the catalyst can react with pollutants. For the same particle shape, smaller particles have a higher ratio of surface area to volume. Thus smaller particles could be expected to require less catalystmass to achieve the same reaction surface area. The increased surface area of smaller particles may not be as meaningful, however, if the particles agglomerate into larger clusters as shown in Fig. 3d.

The initial catalyst mass fraction in PT001 decreases with decreasing particle size, but the fraction of catalyst retained after 20 backpulse cycles increases, from 80% for 75–150μm particles to 98% for<1μm particles. In contrast, the RY806 retains 97–99% of its catalyst loading at all particles sizes. The highest initial catalyst loading (96% mass fraction catalyst) for this fabric is achieved with catalyst particles 10–75μm in size. Larger particles (75–150μm) show slightly lower initial loading (86% mass fraction) and smaller particles (<1μm) show a significantly lower initial loading (51% mass fraction).

It is important to note that the initial catalyst loading achieved using the current process is significantly higher than that of other methods. For example, using RY805 fabric, Hrdlicka et al. (2008) achieved catalystmass fractions between 21 and 24% using a spraycoat method and 17–23% using a double dipcoating method. The current method has achieved in excess of 80% catalyst mass fraction for a variety of process parameters and good catalyst retention during the simulated gas flow testing.

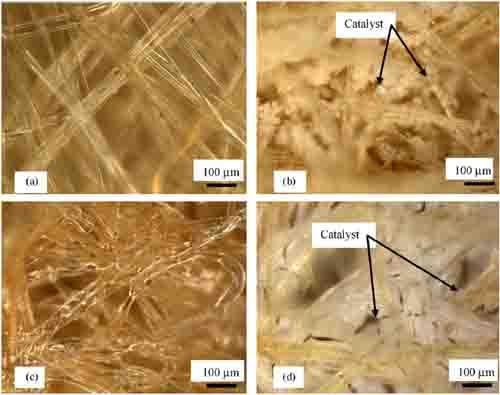
Fig. 3. Darkfield images of (a) pristine PT001, (b) PT001 milled with 10–75μm Al₂O₃ with water, (c) pristine RY805, and (d) RY805 milled with nanometer Al₂O₃ and 70% isopropyl alcohol. Note the agglomeration of nanometer Al₂O₃ into micrometer-sized clumps.

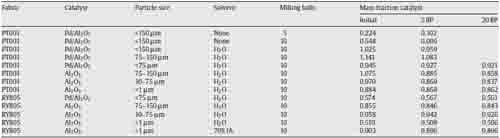
Table 1 – Particle loading and retention with forward/backpulse air cycling. </stron g>

Table 2 – Acceleration data measured from an empty steel milling vial.

Table 3 – Material properties for the steel vial and the PMMA milling balls.

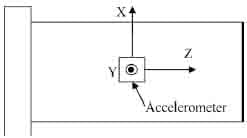
Fig. 4. Orientation of accelerometer axes relative to milling vial.

3.2. Dynamics of catalyst loading process

Details about the forces involved in the process were investigated to give additional insight to the results of Table 1. Information about the motion of the vial during the process was captured by attaching a three-axis accelerometer (PCB Electronics) to the outside of anempty steel milling vial and milling for 1 min. Fig. 4 shows the alignment of the accelerometer axes relative to the milling vial and Table 2 shows the resulting acceleration data.

With the filter samples placed at the bottom of the milling vial, catalyst impregnation will be controlled primarily by the acceleration in the Z-direction. Motion of the vial in the other directions will also influence the motion of the milling balls and will affect the impact energy between the milling balls and the filter fabric. However, without a complete model of the three-dimensional milling spheremotion, estimateswere made of the impact force of a PMMA ball with the wall of the steel milling vial using the accelerations in the Z-direction.

The radius of the contact area between an elastic sphere and a flat elastic plate has been calculated by Young and Budynas (2002) as:

where v1 and E1 are the Poisson’s ratio and Young’s modulus of material 1 and v2 and E2 are the Poisson’s ratio and Young’s modulus of material 2. Using the average maximum acceleration in the Z-direction fromTable 2 and an averagemass of each PMMAmilling ball of 0.54 g, the contact force can be estimated to be 0.19N from Newton’s 2nd law of motion. Both the PMMA and the steel milling vial were assumed to be isotropic with the material properties shown in Table 3.

An estimated contact radius of 0.06mm can be calculated from Eq. (1). Using a contact force of 0.19N and assuming an evenly distributed force, this would be a contact pressure of about 17MPa. This calculation, however, assumes that the milling balls are resting against the vial wall as it is accelerated and hence experience the same acceleration. In all likelihood, the balls will be in motion at the time of impact. Impacts will occur primarily when the ball velocity is in the opposite direction to that of the vial, leading to much higher accelerations for the balls (and hence higher forces) than those measured on the outside of the vial. Therefore, 17MPa is likely a lower bound on the expected contact stresses.

Fig. 5. Impacts on pressure sensitive film on bare steel vial wall after 5 s of milling with (a) 5 PMMA balls and (b) 15 PMMA balls.

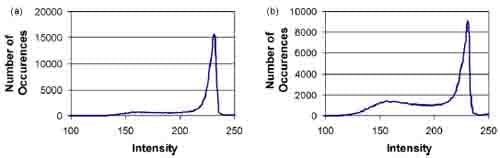
Fig. 6. ImageJ analysis of pressure film results for bare steel with (a) 5 PMMA balls and (b) 15 PMMA balls.

Table 4 – Intensity/pressure equivalents for high film.

It is apparent fromFig. 5 that the milling ball impacts are not uniformly distributed across the base of the milling vial. This is likely due to the nominally horizontal orientation of the milling vial in the mill. Even though the milling motion does subject the vial to significant vertical accelerations (see Table 2), this is not sufficient to evenly distribute the impacts. This was typical of all tests, regardless of the number of balls. Fig. 5 also shows that impacts between the milling balls and the base of the milling vial do not result in a uniform stress, caused by differences in the relative velocities of the vial and milling ball from impact to impact. To quantify the range of stresses, analysis of the pressure film data was performed using ImageJ (2008), a freeware image analysis program available from the National Institutes of Health. The color images were first saved as grayscale and then the intensity of each region tabulated by the ImageJ software. Fig. 6 shows the results for the film samples shown in Fig. 5.

The largest peak in both Fig. 6a and 6b (an intensity > 235) corresponds to the white/offwhite regions of the film that experienced no impacts. Table 4 shows the corresponding pressure at several intensity values. These pressures are determined by comparing the exposed film intensity with a calibration chart provided by the film manufacturer.

The area under the intensity curves of Fig. 6 can be used to calculate an average impact stress for the film. This is accomplished by counting only intensity values < 235 (corresponding to stresses greater than the minimum recommended value for the film). As a result, this calculation ignores regions of the film that experienced no impact. Fig. 7 shows the resulting average stress as a function of the number of milling balls. These results are consistent with the argument that milling impacts are expected to produce contact stresses significantly in excess of 17MPa. They also show that the average impact stress increases as the number of milling balls increases. The presence of additional milling balls may restrict motion of each ball in the X and Y directions, causing ball motion to be directed more purely along the Z-axis, causing larger accelerations, and forces, with each impact.

Due to the much lower stiffness of the filter fabric compared with hardened steel, the presence of filter fabric on the base of the vial is expected to greatly reduce the average contact stress during impact. To confirm this, another round of testing was performed using Pressurex Low Film (2–10MPa) on top of PT001 fabric with 2, 5, 10, or 15 balls. All samples were again milled for 5 s. Fig. 8a and b showthe pressure film results for 5 and 15 balls, respectively. Fig. 9 shows the corresponding average stress as a function of the number of milling balls.

Once again, the average stress increases with the number of milling balls, supporting the results of dry PT001 with 5 and 10 milling balls from Table 1. It seems likely that an optimum number of milling balls exists above which the contact stresses will decrease as motion in the Z-direction begins to be the process are also needed to improve throughput to a commercial scale. One option would be to incorporate a continuous fabric feed mechanism, a solvent/catalyst spray head and a pneumatic milling ball delivery system or even nibbed rollers. Careful control of the milling ball energy will prevent fabric degradation and maximize catalyst loading.

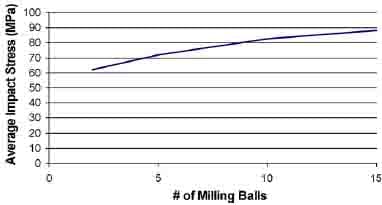
Fig. 7. Average film impact stress as a function of the number of milling balls for high film on bare steel.

Fig. 8. Impacts on pressure sensitive film on PT001 after 5 s of milling with (a) 5 PMMA balls and (b) 15 PMMA balls.

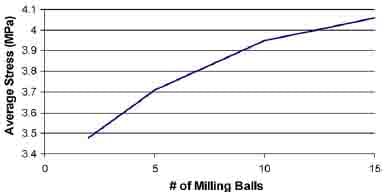
Fig. 9. Average film impact stress as a function of the number of milling balls for low film on PT001.

4. Conclusions

This study has shown that mechanical energy is a viable method for catalyst loading of fabric filters. Specific results of interest include:

1. the presence of a solvent greatly increased catalyst loading andretention;
2. the average impact stress at the fabric surface increased with the number of milling balls;
3. increased average impact stress tended to increase catalyst loading and retention;
4. the PT001 fabric achieved higher initial loading for the smallest catalyst particles (<1μm) than RY805 but both retained greater than 97% of the catalyst after 20 backpulse cycles;
5. the current process can achieve significantly higher catalyst loading and retention than other methods in the open literature.

Additional testing is required to verify the pollution control performance of the catalyst-loaded filters as well as the long-term retention of the catalyst particles. One drawback of the current method is that the distribution of particle impacts over the fiber area was observed to be non-uniform. Significant modifications to the process are also needed to improve throughput to a commercial scale. One option would be to incorporate a continuous fabric feed mechanism, a solvent/catalyst spray head and a pneumatic milling ball delivery system or even nibbed rollers. Careful control of the milling ball energy will prevent fabric degradation and maximize catalyst loading.

Acknowledgments

The authors would like to thank ND EPSCoR for support of Mr. Lilke during the course of the project aswell as funds for equipment and supplies. They would also like to thank Drs. Mike Mann and Wayne Seames of the UND Chemical Engineering Department for constructive discussions during the course of the project and Mike Mays of GE (formerly BHA Technologies) for supplying the filter materials used in this study.

References

1. Brown, T.D., Smith, D.N., O’Dowd, W.J., Hargis Jr., R.A., 2000. Control of mercury emissions from coal-fired power plants: a preliminary cost assessment and the next steps for accurately assessing control costs. Fuel Processing Technology 65–66, 311–341.
2. Hrdlicka, J.A., Seames, W.S., Mann, M.D., Muggli, D.S., Horabik, C.A., 2008. Mercury oxidation in flue gas using gold and palladium catalysts on fabric filters. Environmental Science and Technology 42, 6677–6682.
3. Hylander, L.D., Goodsite, M.E., 2006. Environmental costs of mercury pollution. Science of the Total Environment 368, 352–370.
4. ImageJ–Image Processing and Analysis in Java, 2008. https://rsb.info.nih.gov/ij/.
5. Mann, M.D., Personal Communication, August 2004.
6. “Mercury Study Report to Congress, Volume II,” December 1997. https://www. epa.gov/oar/mercury.html, accessed 9/29/04.
7. “Mercury Study Report to Congress, Volume III,” December 1997. https://www. epa.gov/oar/mercury.html, accessed 9/29/04.
8. “Mercury Study Report to Congress, Volume VII,” December 1997. https://www.epa. gov/oar/mercury.html, accessed 9/29/04.
9. Ness, S.R., Dunham, G.E., Weber, G.F., Ludlow, D.K., 1995. SCR catalyst-coated fabric filters for simultaneous NOx and high-temperature particulate control. Environmental Progress 14, 69–74.
10. Park, O.H., Kim, C.S., 2004. Experimental study on the treatment of volatile organic compound vapors using a photoreactor equipped with photocatalyst-coated fabrics. Journal of Applied Polymer Science 91, 3174–3179.
11. Pavlish, J.H., Sondreal, E.A., Mann, M.D., Olson, E.S., Galbreath, K.C., Laudal, D.L., Benson, S.A., 2003. Status review of mercury control options for coal-fired power plants. Fuel Processing Technology 82, 89–165.
12. Seames,W.,Mann, M.D., Muggli, D.S., Liu,W., 2004. Mercury Oxidation via Catalytic Barrier Filters. Final Report. DOE Contract DE-FG26-02NT41553.
13. Young, W.C., Budynas, R.G., 2002. Roark’s Formulas for Stress and Strain, 7th ed. McGraw-Hill, New York, pp. 702.