Jiyoun Yoo
Abstract
The primary objective of this study was to quantitatively analyze compressive static stress distributions across pallet deck surfaces supporting flexible and rigid packaging in simulated warehouse storage systems. Three different densities of polyolefin foams (2, 4, and 6 lb/ft3, pcf) simulated a variety of flexible and rigid packaging with a range of stiffness properties. A layer of single wall C-flute corrugated fiberboard acted as a sensing medium and also simulated the bottom of a corrugated box. Pressure sensitive films were used to detect compressive static stresses at the interface between the polyolefin foams and the pallet deckboard. Image analysis computer software program was developed to quantitatively characterize stress distributions left on pressure sensitive film. 280 lbs of compression load were applied to a Plexiglas® pallet section (40 x 3.5 inches, L x W) with ¾ inch deck thickness, as well as to a steel pallet section (40 x 3.5 inches, L x W) with ½ inch deck thickness. In both cases, the pallet sections were used in a simulated pallet storage rack. 700 lbs of compression load were applied to the same steel pallet section that was used in the racking simulation and the Plexiglas® pallet sections (40 x 3.5 inches, L x W) with ½ and ¾ inch deck thicknesses were used in simulated block (floor) stack storage to measure the stress distributions and deflections of deckboards. Applying the final models of resultant non-uniform stress distributions enabled the development of finite element analysis (FEA) models of pallet deckboard deflections. The predicted FEA models of the deckboard deflections were validated through comparison with experimentally measured deflections in the simulated warehouse storage systems.
In the final models, the resultant three foams’ stress distributions across pallet deck surfaces in both rack and floor stack storage simulations were non-uniform. The changes in the degree of stress concentrations and maximum stress levels along the deckboards varied, depending on the stiffness of the foams and deckboards and the support conditions in the simulated warehouse storage models. Qualified test indicates that the 2pcf and 4pcf foams represent non-rigid sack products and the 6pcf foam represents rigid packaging and contents. All tests were conducted within a few minutes; hence, all test data were assumed to be initially resulted compressive stresses. The compressive stresses may change over time. The measure of stress concentrations is the stress intensity factor, which is the ratio of initial maximum resultant compressive stress to the applied stress. The initial maximum resultant compressive stresses were adjusted for rate of loading which varied due to the difference in the stiffness of the foams. The table below shows the adjusted initial maximum resultant compressive stress intensity factors. The product of the calculation uniformly distributed compressive stress and the stress intensity factor is the appropriate criteria for designing packaging of product with adequate compressive strength. These factors will be useful when designing pallets, packaging, and unit loads.
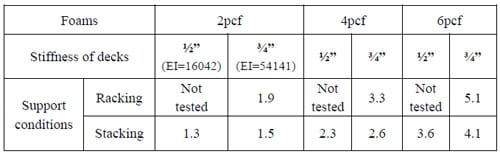
Table Foams
In simulated block stack storage, the foam stiffness (package and product stiffness) had a more significant effect on the stress distributions and concentrations along the deckboards than did the pallet deck stiffness. As a result, the stiffer foam presented a greater change in stress levels along the deckboard under the compression load. The quantified and evaluated stress concentrations and stress distributions will be useful in understanding the interactions between pallets and packaging, reducing product damage and improving the safety of the work place during the long-term storage of the unit loads. The predicted FEA models will allow the industry to better optimize pallets, packaging, and unit load designs.
CHAPTER 1 INTRODUCTION AND OBJECTIVES
1.1 Introduction
All activities within a supply chain involve transferring products from suppliers to customers. In the marketplace, products are manufactured, distributed, bought, and sold according to the principles of supply and demand. Product damage, which is estimated to total $10 billion per year in the United States, largely occurs during the distribution cycle of the supply chain (Clancy, 1988). Products that become damaged during distribution or storage have a significantly adverse effect on the overall supply chain costs. Unit loads can increase the efficient distribution of consumer and industrial products during handling, storage, and transportation.
Unit load is defined as “a single item, a number of items, or bulk material which is arranged and restrained so that the load can be stored, picked up, and moved between two locations as a single mass” (White & Hamner, 2005). The distribution part of a supply chain might include products assembled into unit load form so that handling cost and damage can be reduced. The success or failure of the supply chain distribution system can be determined according to how well the unit load is designed based on the product, packaging, and materials handling equipment. The components within the unit load portion of the supply chain consist of packaging, pallets, and material handling equipment, all three of which physically and mechanically interact during handling, storage, and transportation. Hence, the design integration of these three interactive components will determine the effectiveness and efficiency of the unit load within the supply chain.
Packaging is a critical component in the transportation and distribution environment. Packaging protects products and is a major cost determinant within the logistics system. Recently, the Free Trade Agreement (FTA) has accelerated global transportation and distribution. Packaging design and materials must be engineered into the static and dynamic environment of a unit load to achieve successful global distribution and marketing strategies.
A wide variety of products lead to the production of a wide range of packaging forms. Unpackaged products are exposed to a wide range of environmental hazards, including temperature and pressure change, as well as to external factors, such as the impact of static and dynamic forces during distribution and transportation.
Corrugated fiberboard containers are the most common and significant forms of packaging used for distribution in the United States, accounting for 80 percent of the volume of all paper packaging (Twede & Selke, 2005). In the United States, every product is protected by corrugated fiberboard containers so it can be shipped and stored in warehouses.
In the Unit
ed States, approximately 90% of packaged products are shipped on pallets in the form of a unit load. In the modern supply chain, pallets are used to more efficiently organize and stack products and organize. The economic losses caused by unsaleable products that have been damaged during manufacturing, handling, storage and transporting is one of the most important concerns for reducing costs. According to Clancy, some sources have estimated that poor or improper packaging is responsible for 15% of all damages that occur during shipping; this translates into product damages of about $10 – 30 million annually (Clancy, 1988). Without a systematically well-designed unit load system, any increase in the number of products shipped globally in unit load forms will directly lead to increasing economic losses.
In terms of the interactions between the components within a unit load, particularly between wooden pallets and corrugated fiberboard packaging, previous research has shown that dynamic stresses such as shock and vibration significantly influence interactions between components in unit loads. This previous research evaluated unit loads in simulated handling and transportation environments (Weigel, 2001). Studies evaluating structural interactions between shapes and forms of packaging and pallets in a unit load system are complicated and not well understood, and transportation, storage and distribution systems have been changing quickly over time. Static stresses, especially static compressive stresses caused by the mechanical behavior of the interface between pallets and packaging during long-term warehouse storage, has not been well-documented by experimental research. Non-uniformly distributed compressive stresses imposed by packaging at the interface of pallets and packaging can cause significant economic losses and unsafe working condition in a unit load system.
Understanding the interactions between the primary components in a unit load design will have a significant impact on reducing economic losses caused by inefficiencies in the use of pallets and packaging. Moreover, it will also help improve workplace safety.
1.2 Problem Statement
Non-uniform stress distributions during the stacking of unit loads can lead to economic losses that result from product damage and unsafe working conditions. Figure 1.1 shows compressive static stress distributions during floor stacking storage. Figure 1.1 demonstrates that stress concentrations occur at the interface of the packaging and pallet stringers; these concentrations are caused by the pallet deckboard bending under the weight of the load. Stress concentrations may damage products assembled in unit loads during storage. Figure 1.2 shows a unit load of plastic bottles packaged inside a corrugated box and stacked on a pallet. In this example, the packaging designers did not anticipate the stress concentrations that have occurred in this unit load. As a result, some of the bottles have been damaged at the area of high stress concentrations.
Some possible solutions to this problem would be to increase the stiffness of the pallet decks and the stiffness of the packaging to reduce the stress concentrations over the pallet stringers when these unit loads are stacked. The plastic bottle is the highest cost component in this unit load, but strengthening every corrugated box would also be very expensive; improving the pallet design would be a low cost solution.
The purpose of this research, therefore, is to evaluate and quantify stress concentrations in unit loads at the interface between pallet deck surfaces and product packaging during storage. These results will allow designers to improve unit load efficiency and safety in the work place.
![Figure 1.1Schematic of the simple unit load form. Page 21. [illustration] White, M.S (2007). Unit load material handling interaction. White and Company presentation.Used with permission of Marshall S. White. figure 1.1](https://www.sensorprod.com/wp-content/uploads/2023/09/figure-1-1-1.jpg)
Figure 1.1Schematic of the simple unit load form. Page 21. [illustration] White, M.S (2007). Unit load material handling interaction. White and Company presentation.Used with permission of Marshall S. White.
![Figure 1.2 Non-uniformly distributed loads on packaging and pallet. Page 20. Figure 4. [photograph] White, M. S. (2005). The effect of mechanical interactions between pallets and packaging on packaging costs. Preshipment testing newsletter (4), 18,20,22. Used with permission of Marshall S. White. figure 1.2](https://www.sensorprod.com/wp-content/uploads/2023/09/figure1-2.jpg)
Figure 1.2 Non-uniformly distributed loads on packaging and pallet. Page 20. Figure 4. [photograph] White, M. S. (2005). The effect of mechanical interactions between pallets and packaging on packaging costs. Preshipment testing newsletter (4), 18,20,22. Used with permission of Marshall S. White.
1.3 Objectives
Two commercial computer software packages, CAPE® and TOPS®, allow users to optimize unit load designs in terms of cost and space utilization (Changfeng, 1996). These programs combine unit load components, such as pallets, packaging (both primary and secondary), and materials handling equipment into a geometric “best-fit” (Han, 2007). However, these software packages do not easily predict the structural performance of interacting components in the unit load system. Another drawback of these commercial software applications is that they do not enable the user to simulate the effect of using specific materials and components to protect unit loads from hazards during distribution.
Previous research quantitatively analyzed static stress distributions across pallet deckboard surfaces. In these studies, a predictive mathematical model was developed using finite element analysis (FEA). To simplify the analysis, this model predicted the deflections of pallet decks by compressive stresses utilizing a rigid load (Han, 2007). However, almost all packaged products that are stacked and shipped on pallets have nonrigid loads.
The objectives of this study are to:
- Using pressure sensitive films, quantitatively analyze the compressive static stress distributions across pallet deck surfaces supporting flexible and rigid packaging.
- Simulate the stiffness of flexible and rigid packaging.
- Simulate warehouse storage systems, including:
- Pallet storage rack
- Block (floor) stack storage
- Simulate the stiffness of pallet deckboards
- Using ANSYS, develop finite element models of pallet deckboard deflection by non-uniformly distributed compressive static stresses.
This research will focus on quantitative analysis of compressive static stress distributions on pallet deckboard surfaces that are supporting flexible and rigid types of packaging. The packaging will be simulated using a variety of materials with a range of stiffness properties. Also, this study will simulate pallet storage rack and block stack storage systems, both of which are commonly used in warehouses. To understand the effect of the stiffness of pallet decks on stress distributions and deflections in block stack storage, this study will use two different thicknesses of deckboard.
To characterize static stress distributions across pallet deckboards, the deckboards will be covered with pressure sensitive films. Images on the pressure sensitive film will be analyzed using an image analysis computer software program. The quantitatively characterized static stress distributions will be used to develop mathematical finite element models to predict pallet deck deformation. The predicted deflection models will be compared to experimentally obtained deflections to validate the prediction. A computer software pr
ogram, ANSYS® will be used to generate two-dimensional finite element models, define material and element type, define loads, and predict the deflections of pallet deckboards. ANSYS® is one of many commercial finite element software packages that can solve a variety of mechanical problems, such as static/dynamic structural analysis, heat transfer, and fluid analysis (ANSYS®)
The analyzed stress distributions and predicted finite element models of pallet deck deflections will allow pallet, packaging, and unit load designers to better optimize whole unit loads. This research also has great potential to increase supply chain efficiency for consumer and industrial goods when stack storage compressive stresses are present in pallet storage racks and block stack storage systems.
1.4 Delimitation
This research focuses only on the simplest form of the unit load, in order to better understand compressive static stress distributions over pallet deck surfaces, as well as the resulting deck deflections. A typical unit load includes a full size pallet and multiple layers of products packed in corrugated fiberboard containers. This study will use pallet sections consisting of three stringers connected at the top and bottom. The deckboard will be 40 inches in length and 3.5 inches in width. A layer of corrugated fiberboard pad will be used to simulate the bottom of a corrugated container. This pad will be also function as a sensing medium to indicate stress distributions on the pressure sensitive film. Since corrugated fiberboard is a paper based material, its quality can be easily affected by environmental factors such as temperature and humidity. To control these variables, the study will use corrugated fiberboard that has been stored in the same location under constant temperature and humidity. The study will also use polyolefin foams with three different densities to simulate flexible and rigid packaging with a range of stiffness. The pressure sensitive film that will measure stress distributions can detect forces greater than 2psi.
This research will develop two-dimensional models of a pallet top deckboard; this model will predict deflections caused by analyzed non-uniform compressive stresses. During compression and deflection testing in both pallet storage rack and stack storage simulation, the bottom deckboard would not come into contact with simulated packaged products. In this study, the deflection of the bottom deckboards would be assumed to be the same as those of the top deckboards in pallet storage racks; consequently, only the deflections of the top deckboards will be estimated by modeling using finite element analysis. Also, as the bottom deck would not deflect during the block stack storage simulation, only the top deckboard will be modeled in the block stack storage condition.
CHAPTER 2 BACKGROUND AND LITERATURE REVIEW
2.1 Unit Load System
Pallets, packaging and materials handling equipment all interact with each other throughout the supply chain. A typical unit load consists of corrugated fiberboard containers stacked on a pallet and stabilized with plastic stretch wrap. The unit load system was developed to enable easy and efficient storage and distribution of products through the supply chain. Consequently, most consumer and industrial products are shipped in the unit load form throughout the U.S. It is estimated that two billion or more unit loads are in use on a daily basis (Hamner & White, 2005). According to White, “The unit load would improve the efficiency of storage and shipping space utilization by 6 to 13 percent. This would reduce global wood consumption for pallet manufacture by an average of 6.7 percent of lumber annually and reduce the mass of packaging by 3.2 million tons annually which would in turn reduce packaging cost and fuel consumption (White et al, 2006)”.
There are two fundamental concepts in unit load design: component-based design and systems-based design. Component-based design is the traditional method; in this design, each component of the unit load is developed independently. Component-based design is focused on cost reduction in each component. Since changing the design of one component will influence the performance of other components within the unit loads, the potential consequences of component-based design may include product damage, waste of natural resources, high packaging cost, and occupational injuries that could result from failures during storage and distribution (White, 2007). White et al. (2006) note that 25 % of occupational injuries occur during material handling processes, with over half of those related to packaging failure.
Systems-based unit load design was developed based on an understanding of how the three components of a unit load physically and mechanically interact during transit, storage and distribution. Component interactions considered in the systems-based design include:
- Distribution vibration and unit load resonance
- Load bridging and unit load deformation
- Equipment spans and unit load deflections
- Interfacial friction and load stability
- Compression stress redistribution and product protection
- Vertical stabilization versus horizontal stability (White et al, 2006).
White notes that 12 to 15% of the annual operational expense in the U.S. logistics system can be eliminated using systems-based design instead of component-based design (White, 2006). Furthermore, the systems-based unit load design make it possible to reduce total annual packaging costs by 8 to 18 % (White, 2007).
Analyzing component interactions will help to improve systems-based design. Since the pallet acts as an interface between the packaging and handling equipment in the logistics distribution system, the pallet is the most critical component in systemsbased design.
2.2 Components of Unit Load Portion of Supply Chain
2.2.1 Wooden Pallet
2.2.1.1 Use of Wooden Pallet
A pallet is a flat, rigid, and portable structure on which goods are assembled, stored, stacked and transported as a single unit load. Since the 1940s, the pallet has been a fundamental device used with fork-trucks or hand-jacks in modern material handling systems throughout the world. More than 450 million new pallets are manufactured annually in the United States, and it is estimated that 1.9 billion pallets are currently in use in the United States (White et al, 2006).
Wood has been, and still is, the predominant raw material used in the pallet industry. Although alternative pallet materials such as paper, steel, and plastic have been introduced, wood is still used in more than 90 % of all pallets manufactured today. This is because wood offers relatively high performance at low cost (Twede & Selke, 2005). Wooden pallets are a reusable, repairable, and recyclable device for material handling. The benefits of wood pallets improve the cost effectiveness of unit loads and the material handling environment.
Because wood is a biological material, its physical and mechanical properties are variable. The mechanical properties are affected by natural characteristics such as density, knots, slope of grain, and moisture content. Wood properties are further complicated by its orthotropic characteristics (Bodig & Jayne, 1982). Consequently, the quality of lumber used to make pallets will have a significant effect on their performance during handling, storage, and transportation, and pallet defects that occur during manufacturing can further reduce performance when the pallet is actually utilized. As pallet performance has a significant influence in the efficiency of material handling and entire unit load system, understanding pallet performance is a critical step to improving the performance of the unit load and supply chain system.
2.2.1.2
Wooden Pallet Design
Preliminary studies have revealed that pallet design can affect the performance of the pallet within the unit load distribution environment. Connolly and Lee (2002) found that the natural frequency of unit loads undergoing resonant vibration is related to pallet characteristics. Additionally, stiffer pallet decks tend to have more resistance to bending deflection under load. Pallet decks can be stiffened by increasing joint connection stiffness between the deckboard and the stringers, or by increasing the number of stringers. This, in turn, can protect vibration-sensitive products from becoming damaged during shipping and distribution (Weigel & White, 1999).
An effective pallet design must exhibit a good balance of five interactive parameters: strength, stiffness, durability, functionality, and purchase price. Balancing these parameters is important, as each parameter can influence the others. Pallet users need to know the physical and mechanical characteristics of products and the distribution environment so that they can determine and create pallet designs that balance the five interactive parameters (Clarke, 2004).
The Pallet Design System (PDS®) is a computer-aided design program that assists wood pallet and unit load design. The software was developed with the cooperation of the Pallet and Container Research Laboratory at Virginia Tech and the National Wood Pallet and Container Association (NWPCA). The major difference between PDS® and other similar available computer programs, such as TOPS® and CAPE®, is that, in general, TOPS® and CAPE® help to design unit loads based on the geometric fit of unit load components. PDS® was developed to design pallets based on load type and support conditions, and uses structural analysis of wood pallets to optimize their performance and cost (Loferski, 1987). PDS® is currently being used to design and evaluate pallets throughout the world. By inputting the pallet specifications, PDS’s users can analyze, improve and select a pallet design based on performance and cost. Pallet specifications include the following information:
- Pallet dimension
- Wood species
- Grade and moisture content
- Type of fasteners, fastener lengths and number of fasteners per joint
- Drawings showing deck and stringer configurations
- A bill of materials (Twede, 2005).
If pallet manufacturers specify the information related to pallet components and handling environments, PDS® can estimate the strength, deformation and durability of the loaded pallets; this, in turn, can help maximize design development.
An improper pallet design can result in product damage, tipping stacks, and occupational injuries while pallets are handled, shipped, and stored within the supply chain distribution environment. High quality pallets can be designed by carefully managing pallet specifications to accommodate the packaging and materials handling systems that they will be exposed to.
2.2.2 Distribution Packaging
2.2.2.1 Introduction
Packaging is categorized by levels or functions. The three basic types of packaging are primary, secondary, and tertiary packaging. Primary packaging is the material that contains and directly contacts the product. Secondary packaging is located outside the primary packaging and contains the primary packaging and product. Tertiary packaging is an assembled unit that is handled, stored and shipped. The most typical form of tertiary packaging is boxes assembled in the unit load form (Robertson, 1992). The styles and forms of packaging stacked on a pallet, and the pattern in which they are stacked can affect the entire unit load system. For example, packaging materials with rigid bottom, such as steel drums can pass many more stresses to a pallet than more flexible packaging, such as corrugated boxes (Clarke, 2002). The stacking pattern of packaging types and materials can also affect the stresses on pallet. For example, using the interlock stacking pattern, rather than the column stacking pattern, can reduce stresses on a pallet (White et al, 2006).
Most consumer and industrial product damage occurs during handling, storage, and transportation. This damage has been estimated at $10 billion per year in the United States alone. Of the total product damage, $10-30 million per year are caused by poor or improper packaging during a unit load distribution (Clancy, 1988). Selke (1994) mentions that “The simplest classification divides packaging functions into three areas: protection, communication, and convenience.” Among these functions, enclosing and protecting products is the most fundamental. From point and time of origin to point and time of consumption, packaging should be designed to protect products from any hazards, including external forces, heat and cold, humidity, and corrosion. Primary and secondary packaging forms and pallets all interact within a unit load. Therefore, the performance and efficiency of a load is influenced by the function of both packaging and pallet design.
2.2.2.2 Material for Distribution Packaging: Corrugated Fiberboard
Paper-based packaging accounts for the largest portion of all packaging products. Approximately 70% of paper-based packaging is corrugated fiberboard; folding cartons and setup boxes account for another 20% (Hanlon et al, 1998). The corrugated fiberboard container, or box is the most common type of shipping container, being used today in a palletized unit loads. Most products are packed into corrugated fiberboard containers for protection during handling, storage, and transportation throughout the U.S. and the world. Historically, corrugated fiberboard was invented to protect fragile objects such as glass, pottery, and fruits (Corrugated Packaging Alliance, 2008). However, due to corrugated fiberboard’s strong performance characteristics and ease of handling, its applications are being expanded to almost all packaged products in the supply chain.
Corrugated fiberboard is made of two paper-based materials: one or two flat sheets of paper, called liners, and a corrugated sheet of paper, called the medium. These two components, combined into one structure, make the whole container stronger in withstanding bending stress and pressure from all directions. Corrugated fiberboard is divided into four types, depending on the number of faces and walls: single face, single wall, double wall corrugated, and triple wall corrugated. The thickness of corrugated board is determined in terms of flute sizes and the number of liners. The three commonly used flute sizes applied to the medium are A, C, and B flute, listed from largest to smallest. C-flute single wall board is the most popular flute model for packaging materials. It is characterized by a better stacking strength than B-flute and a better printing surface than A-flute. As the largest and thickest flute, A-flute has good flexural stiffness and compression strength, while B-flute offers a better printability because it is smaller and thinner than A and C-flute. Utilization of these three types of flute varies, depending on the packaged product and level of primary packaging (Twede & Selke 2005).
A specification of the board grade includes the information of the flute type and the basis weight of the medium and of the two linerboards. Different board grades have a significant effect on the corrugated fiberboard container’s performance in the supply chain distribution environment (Armstrong, 2008).
Another factor that can influence the compression strength of the container is the flute rigidity, which is measured by Flat-Crush Testing (FCT). In FCT, crushing force is applied perpendicular to the surface of the board to measure the rigidity of the flute. Crushed board, due to a low FCT, can reduce the stiffness and bending strength of a box. Twede and Selke (2005) note that “
The FCT test is generally used only for single-wall board. A typical FTC for single wall C-flute is 20 psi.” Stiffer medium and good flute formation can result in a high value of FCT.
2.2.2.3 Properties of Distribution Packaging: Compression Strength
Corrugated boxes that are palletized in a unit load form require enough compression strength to bear the weight of loads stacked above them. Pallet loads are often stacked as many as four unit loads high to optimize space utilization during storage. The required compression strength of boxed products for a specific application can be calculated by multiplying the safe stacking load by the safety factor for warehouse floor stack storage. The formula can be written as follows:
Safe Stack Load (SSL) x Safety Factor = Compression Strength
This calculation for compression strength is used to estimate the stacking performance of boxes in transit, distribution, and in warehouse (White et al, 2006). The safe stack load is the loads that can be safely supported by the bottom box (Center for unit load design at Virginia Tech, 2006). A safety factor can be determined based on many environmental factors such as humidity, storage time, pallet pattern, pallet overhang, and vibration. The compression strength of corrugated fiberboard containers can decrease with increased moisture content, storage time, and handling damage (Han, 2006).
The ability of boxes to resist compressive stresses during storage will vary depending on stacking patterns of packaging and stress concentrations caused by the pallet. Therefore, the compression strength of packaging plays an important role in warehouse storage systems. Poorly designed corrugated boxes can fail, cause damage to products and increase the risk of injuries to workers.
2.3 Material Handling Practices
A warehouse is a building used for storing goods. Warehouses allow manufacturers and exporters to store their products before distributing them to consumers. There are three procedures commonly observed in warehouse storage:
- Goods that are produced in a plant and stacked on a pallet are moved into a warehouse using transport equipment, such as a conveyor, fork lift, or pallet truck.
- Shipped packaged products are stored on the floor or on pallet racks in warehouses.
- When the warehouse is ready to release its products to customers, appropriate shipping equipment, such as trailers, rail cars or freight containers, are chosen.
Most packaged product damage occurring during handling and shipping within a unit load form is associated with dynamic stresses caused by shocks and vibrations. Shocks to packaged products mainly result from dropping during manual handling. Vibration damage typically results during transportation (Weigel, 2001).
Static stresses, particularly compressive static stresses, are the major causes of packaging and product damage on a pallet during long-term warehouse storage. In warehouses, unit loads are commonly stored on the floor and stacked on top of each other (Bartholdi & Hackman, 1998). Figure 2.2 shows one loaded pallet high in block stack storage, which is also called floor stack storage. The stacks on the floor generally range from 1 to 7 loaded pallets high. The range can be determined by the weight and stability of the loads, as well as the stiffness, durability, and functionality of the pallets (White et al, 2006).
Pallet storage rack systems are also commonly used in warehouses. Storage racks are composed of several levels of racks that independently support individual palletized unit loads. This storage system makes fork truck access to the loads convenient. Pallet storage racks are more cost-effective and efficient unit load storage method than floor stacking. The different types of pallet racks include:
- Static load beam rack systems (Selective rack, Drive-in, and through)
- Dynamic flow rack systems (Push-back rack)
- Portable rack systems (Integrated Storage Solution, Inc, 2008)
Selective rack is the most popular system used in warehouses. A unit load form supported in a selective storage rack system is shown in Figure 2.3. In this image, the the pallet is racked across the deckboards in the racking system. The pallets are supported between load-supporting beams in the selective rack system, creating high accessibility. Previous research has showed that, in pallet storage racks, higher compressive static stresses occurr around pallet stingers with maximum deflection of deckboards at the center. Also, research has revealed that using a pin joint method for connecting a pallet deck and stringers has shown more deckboard deflection in a storage rack simulation. The same is true of storage rack simulations that use a thinner deckboard. Joint connection stiffness and deckboard thickness have an effect on stress distributions across pallet decks when unit loads are racked (Han et al, 2005).
Loferski et al (1987) developed a method for predicting the structural behavior of stringer pallets that are stored in warehouse racks. This research revealed that pallet top deckboards pivot around the inner edge of the outer two stringers when pallets are racked across deckboards (RAD). In the case of bottom pallet deckboards that are in RAD condition, performance was dependant on the location of the support, the flexural stiffness of the bottom deck, and the magnitude of the unit load. Therefore, pallet storage rack users should specify the limits of deflection and strength for unit loads.
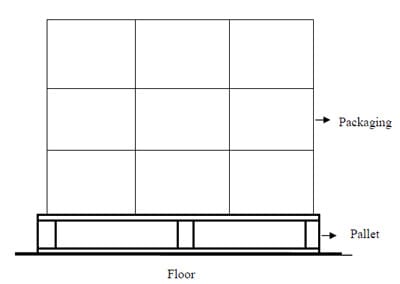
Figure 2.1 Schematic of block stack storage.
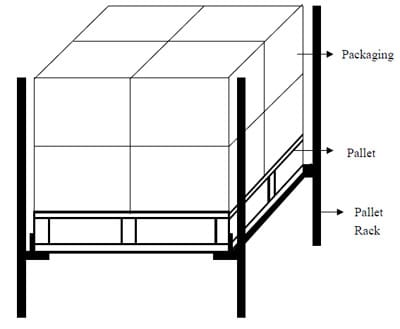
Figure 2.2 Schematic of pallet storage rack system (racked across deckboards).
To avoid product damage occurring from compressive static stresses caused by long term storage unit load floor stacking or warehouse racking, it is important to understand stress concentration locations across pallet decks that support flexible and rigid packaging or other unit loads. The understanding of interactions between the palletized components of a unit load and the materials handling equipment can be improved.
2.4 Modeling of palletized load by Finite Element Method
2.4.1 Finite Element Method
The finite element method (FEM) is one of the most popular numerical analysis techniques used for finite element analysis (FEA). FEA is a computer simulation technique used mostly by engineers, scientists, and mathematicians (Huebner, 1982). FEM was developed to solve complex structural analysis and elasticity problems. Since the 1960’s, its usage has been broadly extended to a variety of fields; most commercial FEM software packages, such as ABAQUS and ANSYS originated in the 1970s (Brebbia, 1974).
The basic principle of FEM is that a complicated structural model can be cut into smaller components, called “elements,” by using a sub-dividing system in which the differential equations obtain the approximate solution. To solve a problem in FEM, the elements must be reconnected by nodes at selected points. The behavior of the entire structure can be determined by the individual behavior of the elements. In general, commercial FEA software contains several different element types and material properties so that users can select input variables.
There are three fundamental procedures used by commercial FEM software to solve a problem: pre-process or structural modeling; analysis; and post processing. These procedures are presented in Figure
2.1. An advantage of FEM software is that it can accommodate complex geometry types, boundary conditions, and loading conditions. While the FEM solution approaches a true solution from underestimated and underconservative results, its numerical approximation may not result in the exact solution (Cook et al, 1989). To verify predicted solutions, FEM results can be compared to experimental results.
2.4.2 FEM Applications for Pallets
Applying FEM to predict the behavior of complex products, like wood pallets, requires the acknowledgment of several difficult variables. For instance, wood is an orthotropic material, which means that it has material properties, such as stiffness and strength, which differ along three mutually perpendicular axes. When the FEM is employed to predict the deformation of wood pallets, users need to account for the fact that orthotropic properties make wood pallets much more difficult to model than isotropic materials. Due to the complex structure and properties of pallets, it is necessary to verify the FEM modeling results with experimental data. In most prior research that has used FEM simulations to predict pallet behaviors, FEA results have been compared to experimental results. Additionally, FEM studies have used various applications of pallet design and analysis.
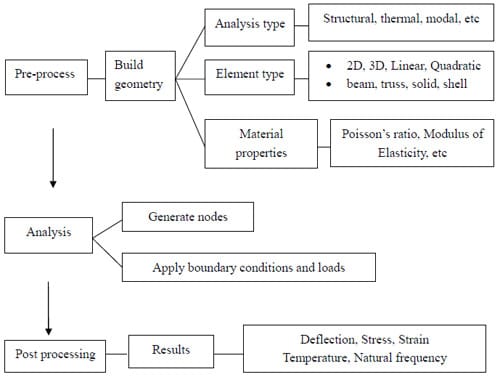
Figure 2.3 FEM procedures by commercial software.
Weigel (2001) developed a FEA (finite element analysis) model to research the dynamic interactions between wood pallets and corrugated containers during resonant vibration within the unit load system. This research resulted in a useful model that was developed to improve the efficiency of the unit load system during transportation and distribution. Using a three-dimensional finite element model, Ratnam (2005) developed a model to predict deformation of a pallet along with several different joint types. This study compared predicted FEM solutions with measurement results for verification. Another study investigated the performance of pallets that are made from several different pallet materials such as plastics, paperboard, and composite materials. The research proposed several optimum designs of the pallet using FEM analysis and simulation (Masood, 2005).
FEM applications for pallet design and analysis in the pallet industry will eventually be increased. Furthermore, applications of FEM for pallet design could potentially improve unit load design, increasing the efficiency of the entire supply chain system.
CHAPTER 3 MATERIALS AND METHODS
3.1 Materials
3.1.1 Construction of Pallet Sample
All pallet section samples used in this research were assembled with one bottom and top deckboard, 40 inches long and 3.5 inches wide, as well as and three stringer segments, 3.5 inches long and 3.5 inches deep, and 1.5 inches wide. The pallet section sample was designed to simulate the GMA (Grocery Manufacturer Association) pallet, the most common size stringer pallet. The GMA measures 40 inches by 48 inches (MHIA, 2008). The test used three different pallet section samples, in which each deckboard component was constructed from ½ inch thick cold roll steel, ½ inch, and ¾ inch thick Plexiglas® (manufactured by Spartech Polycast Co.). Plexiglas® is made of an acrylic base plastic material. It was selected for a deckboard material instead of wood, as its surface is more even and its physical properties are less variable. The major physical properties of Plexiglas® are presented in Table 1 in the Appendix, and the specific purpose of choosing each specimen will be explained in the testing procedure section. For the stringer segment materials, oak and eucalyptus were chosen and applied to Plexiglas® and cold roll steel deckboards, respectively. Smooth shank nails, 2.125 inches long and 0.113 inch in diameter, were used to connect the oak and Plexiglas®. 2 inchlong # 6 screws were used as the fastener between the steel deckboard and the eucalyptus stringers. All pallet section samples used a semi-rigid joint connection method (either nailed or screwed joints) to link the deckboards and stringers.
3.1.2 Pressure Sensitive Film
This study used Pressurex®, a pressure sensitive film manufactured by Sensor Products, Inc., to identify compressive static stress distributions across the pallet deck and packaging interface. When it is placed between any two objects at contact, the film uses a variable darkness level to reveal pressure distributions. The darker the film image, the higher the pressure. The pressure sensitivity of the film can vary from 2 to 40,000psi (Sensor Products, Inc, 2008). Since the actual stress occurring in the warehouse block stack storage and the pallet rack storage ranged approximately from 2 to 6psi, this study used Pressurex-micro®, the micro sensitivity pressure film, which has a detecting range from 2 to 20psi.
The Pressurex-micro® has three distinct layers: a clear plastic Mylar sheet overlaying carbon layer, which is a combination of thick white paper and black carbon, and an adhesive layer. The adhesive layer has three sub-layers within itself: a protective release liner covering an adhesive coated white paper backed by a thick white stock (How to use Pressurex-micro®).
3.1.3 Corrugated Fiberboard
The study used single wall C-flute corrugated fiberboard with grades of 35-26C- 35 as a testing material. The most widely used type of corrugated fiberboard for packaging materials, the single wall C-flute corrugated fiberboard was used not only to detect static stress distributions over pallet deckboards and pressure sensitive films but also to simulate the bottom of a corrugated box, the most commonly used packaging material. As discussed in section 2.2.2.2, the typical FCT (flat crush testing) of single wall C-flute is 20psi, and the pressure sensitive film is able to detect up to 20psi. As a testing material, single wall C-flute corrugated fiberboard has the greatest potential to measure compressive static stress distributions of the sort being generated in this study.
3.1.4 Simulation of Products: Polyolefin Foam
Three different densities of CelluPlank® polyolefin fabrication foam (manufactured by Sealed Air®) were applied to simulate the various stiffness of packaging. In the previous study, rigid loads were assumed and applied on the pallet deckboard to simplify the analysis of compressive static stress distributions and deflections (Han et al, 2005). In this study, however, non-rigid loads were applied by compressing foams in order to simulate non-rigid packaging, as opposed to rigid loads. The three foams, 220, 400 and 600 had densities ranged from 2.0 to 2.4, 3.8 to 4.4 and 5.8 to 6.4 lb/ft³ (pound per cubic foot, pcf), respectively. These were applied over corrugated fiberboard pads, pressure sensitive films, and pallet decks. The density range is based upon ASTM D3575-00 tests that Sealed Air® uses on its product. Detailed information on the physical properties of CelluPlank® is provided in Table 2 in the Appendix.
3.1.5 Flour
Seven identical flour sacks (manufactured by Kroger®) were used to perform the compression testing. The compressive static stress distributions of compressed flour sacks on Plexiglas® pallet deckboards were analyzed. The primary packaging material of the flour was constructed from paper-based material. Each bag of flour was 6 inches long, 4 inches wide, and 2.5 inches deep, and weighed 32oz. (2lb.).
3.2 Testing Method
3.2.1 Calibration Curve
The distributed stresses along the pallet deckboards and polyolefin foams were evaluated using calibratio
n curves. Figure 3.1 shows the testing setup for generating a calibration curve. For the test, a sheet of pressure sensitive film (5.5 x 5 inches, L x W) was placed on the bottom of a steel plate on the testing table, and then a little piece of a corrugated fiberboard pad (4×4 inches, L x W) was applied as a cover over the film. Polyolefin forms (4x4x2 inches, L x W x D) and a rigid steel tube load applicator (7.5 x 5 inches) were applied over the corrugated pad and the pressure film, after which compression loads (speed: 0.5in/min) were applied by a 826.75 MTS servo-hydraulic with 5 kip Interface load cell model # 661.20E-01. The compression loads were applied with several increased levels ranging from 50 to 450 lbs (approximately 3 to 28psi). The specified load levels used for the tests are presented in Chapter 4 and Table 3 in the Appendix. For the overall testing, three different densities of foams were used as the testing treatments. Two replications were performed at each load level with each of three foams.
3.2.2 Simulation of Pallet Storage Rack
For the simulation of the pallet storage rack condition, compression loads were applied to the samples on two-end supports (a I-beam consisting of a bottom flange measuring 6 inches, a top flange of 3 inches, and a web of 6 inches) using the 826.75 MTS servo-hydraulic with 5,000 pound interface load cell model # 661.20E-01. Figure 3.2 shows the testing setup for simulating the pallet storage rack. A simplified schematic of the testing setup is illustrated in Figure 3.3.

Figure 3.1 Testing for generating a calibration curve.
A stripe of a pressure sensitive film was applied over the top deck of each pallet section so that the film covered the entire top deck surface area. Then, a layer of single wall C-flute corrugated fiberboard, 40 inches long by 3.5 inches wide was applied. Its length was placed in a direction parallel to corrugation axes, over the pressure film. Ten blocks of polyolefin foam with varying densities (4 x 4 inches with a thickness of 2 inches for each block) were applied over the corrugated fiberboard pad to simulate the various packaging stiffness. For a compression load applicator, a rigid steel tube spanning the length and width of the pallet section was then applied to the samples.
Since the Plexiglas® pallet section was not stiff enough over the two-end supports to generate measurable contrast within the range of the pressure film on high compression loads, a steel pallet section sample was used with these loads. Loading with the 5 kip load cell was halted after reaching a load consistent with 1,500lbs (approximately11 psi) for the steel pallet section sample. To predict the actual stresses distributed over the deck during the simulated pallet racking, a 280lb (approximately 2 psi) compression load was applied to the Plexiglas® pallet section with the deck thickness of ¾ inch.
The deflection of the Plexiglas® top pallet deckboard was measured during compression testing. An LVDT (linear variable distance transducer) was used to measure the deflections of the pallet deckboards at five locations along the top deckboard component. From the left end of the sample, these were placed at locations of 0.75 inches, 10.25 inches, 20 inches, 29.75 inches, and 39.25 inches. 1 inch, 2 inches, and 0.5 inch Schaevitz LVDT Models (refer to Figure 3.3 for detail), were installed and the deflections of the top deckboard component were recorded automatically through the computer software program LabVIEW®. The model numbers for 0.5, 2, and 1 inch LVDT are 500HR-DC with a working distance of +/- 0.5, 2000HR-DC with a working distance of +/- 2, 1000HR-DC with a working distance of +/- 1 inch, respectively. The pallet section samples made of Plexiglas® deckboards were tested three times for each of the three different density foams to measure deflections.
3.2.3 Simulation of Block Stack Storage
Figure 3.4 shows the testing setup for simulating block stack storage. To simulate block stack storage in a warehouse, the two-end supports that were used for the simulation of the pallet storage rack were removed from the test setup. 4pcf and 6pcf foams over the steel pallet section were compressed by a 1,500lb load.

Figure 3.2 Testing setup for a simulation of pallet storage rack.
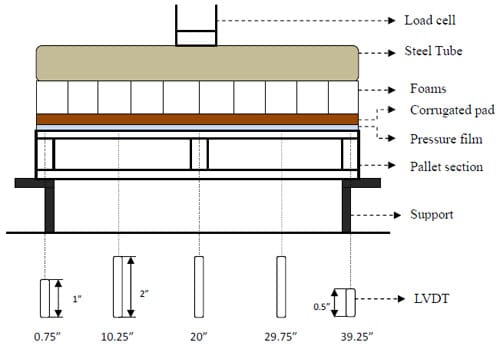
Figure 3.3 Schematic of testing setup for a simulate pallet storage rack.

Figure 3.4 Testing setup for a simulation of block stack storage system.
Plexiglas® pallet samples with deck thicknesses of both ½ inch and ¾ inch were utilized to compare the three foams’ stress distributions and deflections, depending on the pallet deckboard thicknesses in the block stack storage condition. In warehouse storages, heavy unit loads result in stresses of approximately 2psi to 5psi. For the block stack storage simulation, a maximum loading of 5psi (approximately 700 lbs) was applied to the samples. All testing procedures of the block stack storage condition except for the applied load levels and the support conditions were the same as the simulated pallet storage rack. Each Plexiglas® pallet section sample was tested three times, with each of the three different foams, as performed in the pallet rack simulation testing. The testing for the steel pallet sample also had three replications with each of the 4pcf and 6pcf foams.
3.2.4 Flour Sacks
The compression testing was conducted with flour sacks in both simulations of the pallet storage rack and the block stack storage to predict how real packaging would behave in a real storage environment. This testing was for analyzing compressive static stress distributions of the flour packaging over pallet deckboards. Figure 3.5 presents the compression test setup of flour sacks. Seven sacks of flour over a pressure sensitive film and a corrugated fiberboard pad were placed on the ¾ inch Plexiglas® pallet sample and compressed with 280lbs of load in the pallet storage rack testing. For the block stack storage simulation, the seven flour sacks were tested with a 700lb compression load over ½ inch and ¾ inch Plexiglas® pallet deckboard samples. Each of the three tests with the three foams had three replications. The analyzed stress distributions from the flour packaging were compared to the three foams’ results. The deflection of a deckboard was not measured with this flour packaging test.

Figure 3.5 Compression Testing setup for flour sacks in block stack storage condition.
3.3 Modeling
3.3.1 Introduction
In this study, a numerical analysis using the finite element method (FEM) was applied to predict the result of a pallet deckboard deflection by applying analyzed nonuniform compressive static stress distributions imposed by supporting flexible and rigid packaging. As discussed in the literature review section, the struct
ure of a pallet, which consists of several components, has complexities that need to be modeled. Therefore, the experimentally obtained results of deckboard deflections were compared to simulated results using the finite element analysis (FEA) modeling. For modeling the pallet, the study used a commercial FEM software, ANSYS® 9.0 ED Version. In the following sections, geometry creation, material type selection, meshing, and boundary conditions are discussed in terms of modeling procedures. Defining loads will be presented and discussed in Chapter 4.
3.3.2 Geometry Construction
For modeling a deflection of a top pallet deckboard, a two-dimensional (2-D) solid rectangle was created on the work plane of ANSYS. The Plexiglas® pallet sections were 40 inches long by 3.5 inches wide with deckboard thickness of ¾ inch and ½ inch. The two 2-D solid rectangles, 40 inches long by 0.75 inch wide ( Figure 3.6) and 40 inches long by 0.5 inch wide, were generated on the x and y-plane to be modeled so that the vertically deformed shape of the top deckboard could be predicted in the front view of the pallet section sample.

Figure 3.6 The 2-D front view of top deckboard geometry built in ANSYS.
3.3.3 Material Definitions
For the next step of modeling, the structural analysis and the h-method were selected for the analysis and the mesh refinement methods, respectively. The h-method is generally used to increase the number of nodes by reducing the element size without changing the element type. Achieving a successful FEA model requires selecting an appropriate element type, a mesh density, and the number and size of the elements.
PLANE 42 was selected to define the element type; it is generally used for 2-D modeling solid structures. The element type was applied as a plane stress and defined by four nodes, each of which had two degrees of freedom. The plane stress usually occurs in situations where one dimension is so small in relation to the other two, as in the case of a flat or thin element (Bodig & Jayne, 1982). In this study, the plane stress with deck thickness of 0.05 inch and 0.75 inch was assumed for modeling since the thicknesses of Plexiglas® deckboards are thin in the y-coordinates. The Plexiglas® used for the pallet deckboard material was assumed as a linear isotropic material with modulus of elasticity (MOE) of 4.4 x 105 psi and Poisson’s ratio of 0.30 applied to define material properties.
3.3.4 Mesh Generation
Meshes were generated by 0.25 inch by 0.25 inch square elements on the 40 inches by 0.75 inch (Figure 3.7) and 40 inches by 0.25 inch simple solid 2-D rectangular structures. Generally, finer meshes with smaller element sizes result in more accuracy in the FEM approximation. To determine a proper element size of this model, several trials were performed with a range from 0.075 to 0.375 inch square elements. Among the trials, modeling using an element size of 0.25 inch by 0.25 inch resulted in the closest results to experimental results. All elements were connected by nodes, whose numbers were recorded automatically by ANSYS.
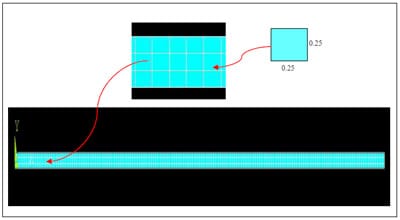
Figure 3.7 Meshed front view of pallet deckboard model.
3.3.5 Boundary Conditions Definition
The determination of boundary conditions depended on the support conditions of the simulated pallet storage rack and the block stack storage conditions. However, as all pallet components were assembled using the same semi-rigid joint connection method boundary conditions were identically applied in terms of the joint method for all models. For modeling the semi-rigid joint there should be no displacement for all degrees of freedom at the outer and inner edges of the stringers by which the stiffened joint connection can be indicated.
Figure 3.8 illustrates the applied boundary conditions in the pallet storage rack simulation. Two outer stringers, 1.5 inches in depth, of a pallet section sample were supported by two-end supports. In the left half of the section, the outer edge (zero point in x and y-coordinates) and the inner edge (6th node from the end at zero in y-coordinates) of the outer stringer were fixed with zero displacement for all degrees of freedom. Boundary conditions in the right half of the section were symmetrically applied.
Figure 3.9 shows the applied boundary conditions in the simulated block stack storage condition. There are three supports (three stringers), consisting of two outer and one inner supports. All outer and inner edges of the three stringers were modeled with zero displacement for all degrees of freedom. Boundary conditions applied in terms of the displacement constraints of the outer stringers were the same as in the pallet storage rack simulation. The inner stringer of the pallet section has zero displacement at the 3rd node at zero in the y-direction from the center of a FEA model for both ways.

Figure 3.8 Boundary conditions in simulated pallet storage rack.
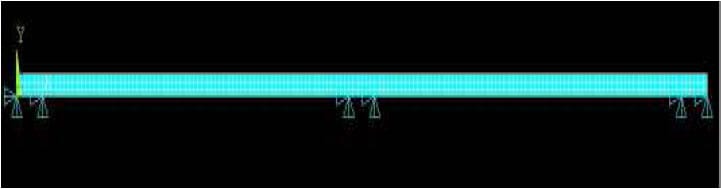
Figure 3.9 Boundary conditions in simulated block stack storage.
3.4 Analysis of Film Image
3.4.1 Introduction
Compressive static stress distributions were detected and analyzed using images left by C-flute corrugated fiberboard pads with loads on pressure sensitive films. A typical image after compression is presented in Figure 3.10(a). The stripes obtained from the impression of a corrugated fiberboard medium are presented in a direction parallel to the cross-machine direction. There were generally ten black stripes generated on a film image, excluding two outer edges, as seen in the enlargement image in Figure 3.10(b).
The thickness (or width) of each stripe at each location along the pallet deckboard was measured and averaged using an image analysis computer software program. The program, developed for this research by Lee (2008), is not commercially available. It was designed to count the number of pixels in black stripes on the film image so that the average thickness of ten black stripes at each given location was measured within designate standards. This image analysis program was designed so that the average values of width fell within the interval W ± s. The levels of the applied compressive static stress at each location were analyzed based on the different thicknesses the lines, which the program measured by counting pixels.
3.4.2 Image Analysis by Program
Using the program, the analysis of images on pressure sensitive films can be completed in three steps, as shown in Figure 3.11. The program consists of two different areas of the window, the view window and the result window. First of all, images on the films must be scanned using a scanner. The software program allows the scanned image files to be opened through the view window, as shown in the second step in Figure 3.11. Subsequently, users can select specific areas for analysis. The properties of the program, including a threshold, minimum and maximum width, can be controlled and vary depending on users. Details of the threshold will be explained in section 3.4.3
of this chapter. The values of properties should be constantly maintained during analysis of all of the images. The results between images would be incorrectly derived unless users ensure this step before selecting the areas. Throughout all image analysis in this research, the threshold value of 60, minimum width of 8, and maximum width of 32 were constantly applied.
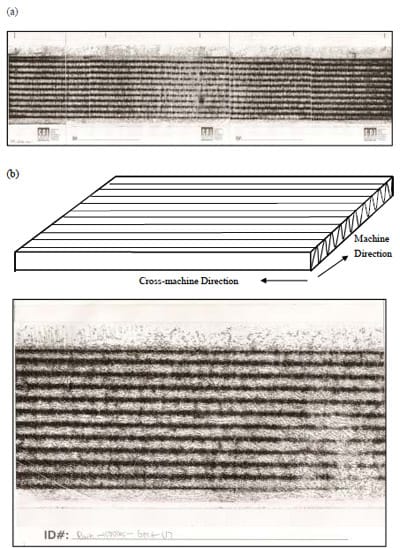
Figure 3.10 (a) Typical image after compression (b) Enlargement of image: Corrugated board placed in the direction parallel to corrugation axes (Cross machine direction).
Once the areas are assigned for analysis, the program automatically starts counting pixels within black stripes at each location along the scanned pressure films. In so doing, it measures the width of each stripe and taking the average of the measured width in selected areas. Afterwards, another window, as seen in the last step in Figure 3.11, shows the results from the analysis of the average width. However, the results given from the result window do not provide details for the width average measured at each location along the deck. While the image analysis is processing, the program saves various data details, such as the average width, the standard deviation, and the number of counted stripes as a function of given location. It also saves images that can be used to verify the analysis.
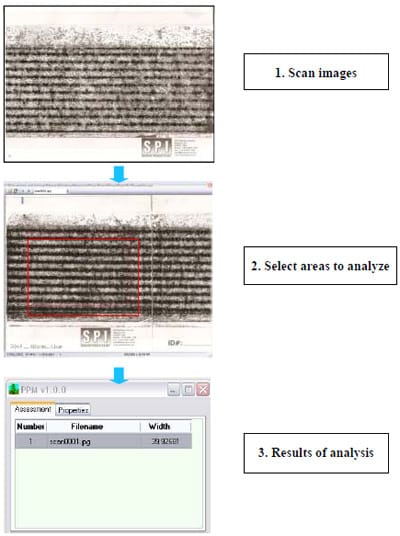
Figure 3.11 Procedures of image analysis by program.
3.4.3 Details of Data Analysis
Figure 3.13 presents the saved text file, including the tabulated data, in terms of the detailed average width at given locations in selected areas, as shown in Figure 3.12. In the details of the text file “ln” stands for line numbers measured in pixels width. For example, the line number “80” indicates the 80th pixel in the horizontal direction (xcoordinates) of the entire image. The unit of the line numbers, “pixel”, can be converted into “inches” using the following formula:
Total length of scanned image (inches) x Line number (pixels)
The number of total pixels in x-direction of scanned image
The number of total pixels in the scanned image is described in Figure 3.12. Thus, the location of line number 80 can be calculated by the total image length of 8.5 inches, multiplying the line number of 80 and dividing by 1711, the total counted pixels in the xdirection. Therefore, the line number 80 is 0.397 inch from the zero point of the entire scanned image in the x-direction. “Avg” in Figure 3.13 means the average thickness of black stripes at each given line number, “std” means the standard deviation of the width, and “count” means the number of “counted” black stripes at each line number in the selected areas. The program automatically excludes the results of width that fall in the outlier of W ± s.
For all tabulated results “noise” is removed from the original images by applying two filtering methods: the smooth version and the black/white version as shown in Figure 3.14. The two images in Figure 3.14 present the same area as selected in Figure 3.12 with filters applied. Figure 3.14 (a) presents the smoothed version and Figure 3.14 (b) shows the black and white inverted image after smoothing. The smooth version can be filtered using the threshold to convert it into the black/white version. Below the threshold value assigned for the image processing in the program, black lines are converted into white lines. Conversely, above the threshold value, white lines are converted into black lines. Thus, the higher threshold value causes thicker white lines in the black/white version. The most adequate threshold value can be determined when the white lines have the least noise, are not too thick or thin.
Figure 3.15 shows the verification for the image filtering process, which is used to validate results. White lines inside black stripes in both the original (Figure 3.15 (a)) and smooth images (Figure 3.15 (b)) indicate the counted lines and width midpoint. These images were useful in verifying and comparing original images and filtered images, making it possible to reduce errors.
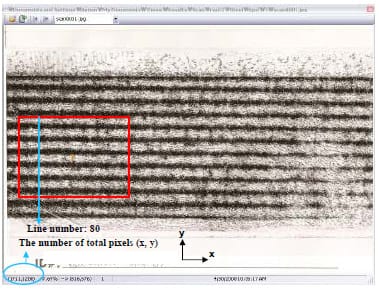
Figure 3.12 Selecting areas by program.
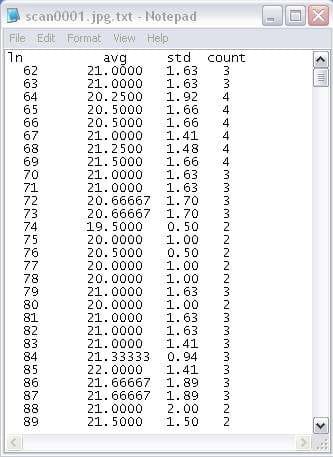
Figure 3.13 Tabulated results from image analysis.

Figure 3.14 (a) Smooth version (b) Black and white version.

Figure 3.15 (a) Verified on original image (b) Verified smooth image.
CHAPTER 4 RESULTS AND DISCUSSIONS
4.1 Introduction
The primary focus of this research was to quantitatively analyze the compressive static stress distributions across a pallet deckboard during long-term warehouse storage. Using the resultant stress distributions, deflections of the pallet deckboard were predicted using FEM. Experiments simulated both pallet storage rack and block stack storage conditions. In this chapter, the predicted finite element models of pallet deckboard deflection were compared to experimental results. The results presented in this chapter are divided into four sections, each of which contains the following information:
- Calibration curve: Results obtained from testing for generating a calibration curve are shown and discussed.
- Compressive static stress distributions: Stress distributions of three different foams and flour sacks across a pallet deckboard in both simulated pallet storage rack and block stack storage conditions are described and discussed.
- Deflection of deckboard: Experimentally obtained results of deckboard deflections are presented and discussed.
- FEA modeling: Results of predicted deckboard deflections obtained from FEA modeling are presented and discussed. A comparison between the experimental and predicted results of pallet deck deflections are described and discussed.
4.2 Calibration Curve
The data used for generating a calibration curve are shown in Figure 4.1. In the figure, stress levels were indicated as a function of the average thickness (width) of black stripes presented in pressure sensitive film images. The stress levels indicated in pound per square inch (psi) were generated by converting the unit of applied compression loads in lbs into the unit of stress in psi. The information, including the specified average width at compression loads (lb.) and stress levels (psi) are provided in Table 2 of the Appendix.
A comparison of calibration data obtained from 2pcf, 4pcf, and 6pcf foams’ compression testing (Figure 4.1) indicates that the resulting data of the stress levels versus the average width for the three foams linearly increases until the co
mpressive stress reaches 20psi, at which point there is a sharp jump in the average width. This sharp increase occurs because the corrugated fiberboard pads start getting crushed confirming the claim that the crush point for single wall C-flute in a crush test is 20psi, as reviewed in Chapter 2 (Twede, 2005). Since the crushed corrugated fiberboard reduces the overall box stiffness during storage, packaging designers do not expect the collapse of corrugated containers in a real distribution environment. Therefore, the test data obtained after the collapse of the corrugated pads were discarded for generating a calibration curve. Also, the resulting width/stress curve had a similar tendency between 2pcf, 4pcf, and 6pcf foams, so all test data were integrated into one calibration data. Figure 4.2 shows the resulting calibration equation. The generated linear calibration equation was used to interpret all experiment results except for the 6pcf foams tested in the stack storage condition. The calibration curve could predict compressive static stress values “y” as a function of the average width values “x” at each location along the pallet deckboard.
A calibration curve for the 6pcf foams tested in the block stack storage simulation was separately regenerated since the corrugated fiberboard was reordered from another manufacturer and used for the 6pcf foam compression tests in the stacking simulation. As the quality of new corrugated board might differ from the previously used board, another calibration curve was generated to interpret the 6pcf foam stress distributions in the block stack storage simulation. The resultant linear calibration equation from 6pcf foam compression testing is presented in Figure 4.3.
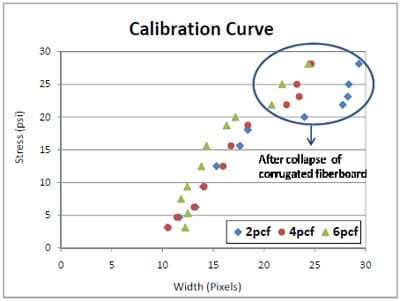
Figure 4.1 Calibration results for three foams.
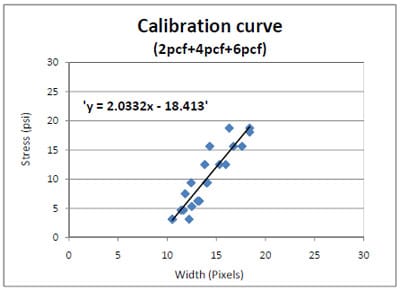
Figure 4.2 Calibration curve indicated by a linear equation.
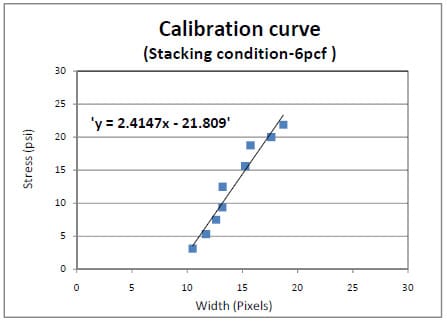
Figure 4.3 Calibration curve for 6pcf in block stack storage condition
4.3 Stress Distributions
4.3.1 Simulated Pallet Storage Rack Condition
4.3.1.1 Introduction
Initially, a Plexiglas® pallet section sample with ¾” deck thickness was placed on two-end supports in a simulated pallet storage rack. Because the Plexiglas® pallet was not stiff enough in this simulation, no measurable stress distributions were found around the center of the deckboard (Figure 4.7). Therefore, a stiffer pallet deckboard material was needed. Cold roll steel was used instead of Plexiglas® so that the three foams’ stress distributions could be traced along the steel pallet deckboard for an analysis of a simulated pallet storage rack condition. Results from these compressive static stress distributions across a steel pallet deckboard were used to generate functional forms that could predict stress distributions across a Plexiglas® pallet deckboard.
4.3.1.2 2pcf Foam
The stress distributions resulting from a 1500lb (approximately 11 psi) compression load applied to 2pcf foams over a steel pallet deckboard are presented in Figure 4.4. Figure 4.4 shows three replications of the test results. As indicated in Figure 4.4, stresses were non-uniformly distributed along the steel pallet deck; that is, higher stresses were more concentrated around two outer stringers than around the inner stringer.
It was assumed that the stresses, occurring on the area where two outer stringers contact the deckboard and are stiffened due to nailing, had uniform distribution. Since the two outer stringers were supported by two end-supports in a pallet storage rack, there might be no deckboard deflection and stresses could be distributed uniformly within this area. However, images on pressure sensitive films after compression testing showed that, due to the nails, there were non-uniform stress distributions over the two-end supports. The nails produced noise on film images; the areas surrounding them included more pixels than expected. Therefore, after analysis, the outer most compressive static stress levels at point 0 to 40 inches were applied to points 0 to 1.5 and 38.5 to 40 inches in xdirection of deckboard location, respectively, rather than from the initially derived results.
Theoretically, the results of compressive static stress distributions for the left and right halves of the pallet section were thought to be symmetrical. However, as seen in Figure 4.4, the analyzed stresses were not symmetrical. The load applicator may have been skewed during testing. Also, pallet deckboards and nails were assembled by hand, creating another possible cause for the asymmetry. Hence, the stress distributions obtained from each half of a section were analyzed individually. The trend of stress distributions at each side was described by third order equations, as shown in Figure 4.5. Stress levels were calculated using the third order equations for both halves at one inch intervals, as tabulated in Table 4.1. The average stress levels of both sides at each interval were assumed to be symmetrical. Thus, the average values in Table 4.1 were used to generate a final model of resultant stress distribution from the edge to the center of the steel pallet deck as shown in Figure 4.6. This final model became a functional form of 2pcf foam. The third order equation of functional form was fitted into the test data obtained from 2pcf foam stress distributions over a Plexiglas® pallet section.
Figure 4.7 shows stress distributions of 2pcf foams compressed by 280 lbs (2psi) load over a Plexiglas® with deck thickness of ¾” in a pallet storage rack simulation. The results revealed that the impressions of the corrugated fiberboard medium could not be obtained from the center of the deck on film since the Plexiglas® deckboard was too flexible. Because the pressure sensitive film was not sensitive enough to detect less than 2psi stresses, thee measurable test data explained that the compressive stresses between the two outer stringers were lower than 2psi. Therefore, 2pcf foam stress distribution across a Plexiglas® pallet deckboard was predicted using the functional form.
Figure 4.8 shows the final model of resultant 2pcf foam stress distribution from the edge to the center of a Plexiglas® pallet section with a deck thickness of ¾”. The final model was generated by fitting the functional form into the test data in Figure 4.7. For the y-intercept of final model, the y-intercept value (at x=0) of the functional form was substituted by the average of the two outer most stress levels obtained from the test data in Figure 4.7. Predicted stress values of less than zero in x-direction were assumed to be zero when the final model was applied to FEA modeling.
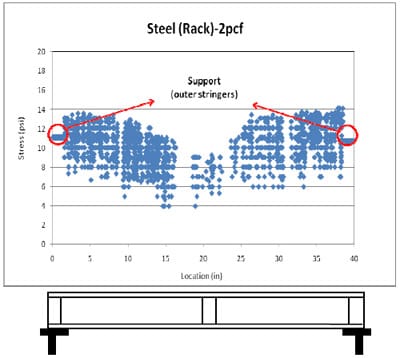
Figure 4.4 2pcf foam stress distribution across a steel pallet deckboard in simulated pallet rack storage.
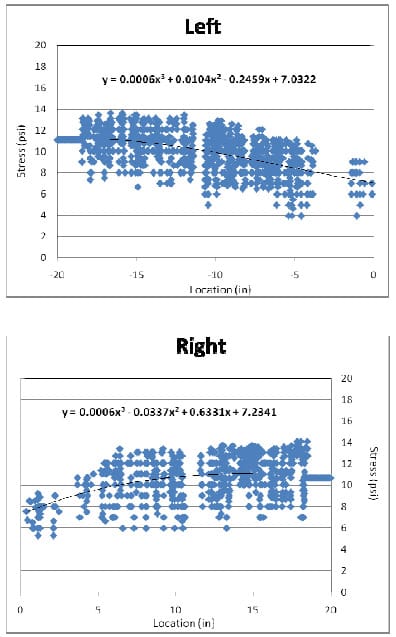
Figure 4.5 Stress distributions and fitting a functional form to the data at le
ft and right of the pallet section.
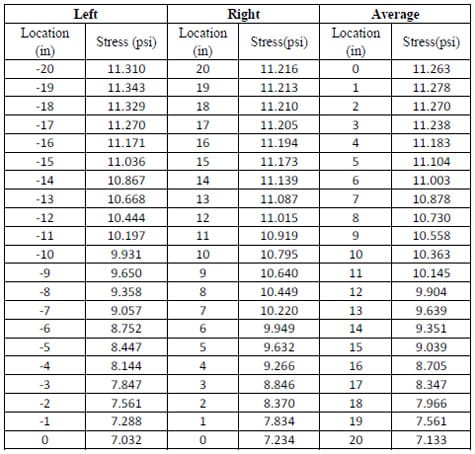
Table 4.1 Tabulated stress distributions by functional foam at left and right of pallet section and the average stress of both sides.
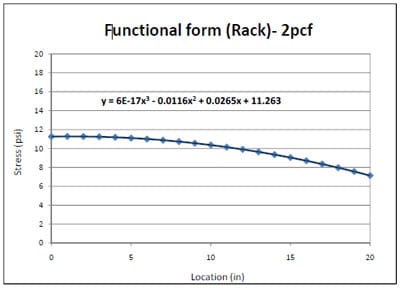
Figure 4.6 Functional form of resultant 2pcf foam stress distribution from the edge to the center of a steel pallet deckboard in simulated pallet storage rack.
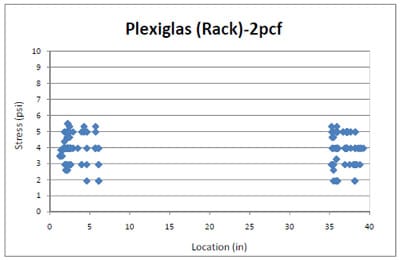
Figure 4.7 2pcf foam stress distribution across a Plexiglas® deckboard in simulated pallet storage rack.
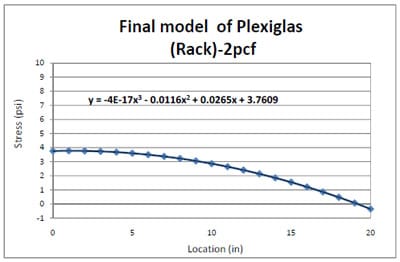
Figure 4.8 Final model of resultant 2pcf foam stress distribution from the edge to the center of a Plexiglas deckboard.
4.3.1.3 4pcf Foam
The 4pcf foam compressive static stress distributions in the pallet storage rack condition were analyzed using the same procedures that were used for the 2pcf foam analysis in the preceding section. Figure 4.9 shows the three replications of the 4pcf foam stress distributions across a steel deckboard in a pallet storage rack simulation. Figure 4.10 presents the generated resultant functional form, based on the 4pcf foam stress distribution test data. Higher stress concentrations occurred around two outer stringers over the pallet deck in the pallet storage rack and the highest stress level was approximately 11 psi. The level was similar to the highest stress level from the 2pcf foam stress distribution. From the results, it was observed that packaging with stiffness between 2pcf and 4pcf foams does not have an effect on the trend of stress distributions and degree of stress concentrations around the two outer stringers.
Figure 4.11 presents the results of 4pcf stress distributions across a Plexiglas® pallet deckboard in a simulated pallet storage rack. The result of 4pcf foam test data was similar to the result of 2pcf foam stress distributions (Figure 4.6) over a Plexiglas® pallet deckboard. Figure 4.12 shows a final model of resultant 4pcf foam stress distributions, predicted using the generated functional form in Figure 4.10. This final model demonstrated that the stress level at the center of the deckboard was 92% lower than the stress level at the edge. The resultant final model was also used to predict the Plexiglas® pallet deckboard deflection using FEA modeling.
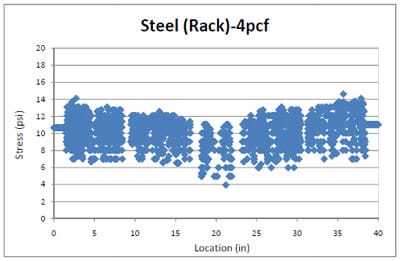
Figure 4.9 4pcf foam stress distribution across a steel pallet deckboard in simulated pallet rack storage.
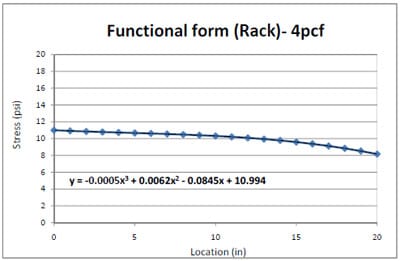
Figure 4.10 Functional form of 4pcf foam stress distribution from the edge to the center of steel deckboard in simulated pallet storage rack.
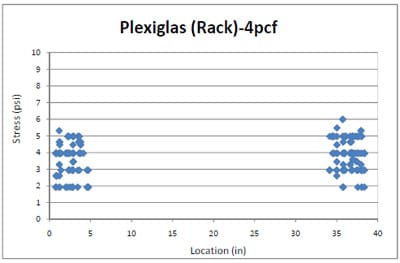
Figure 4.11 4pcf foam stress distribution across Plexiglas® deckboard in simulated pallet storage rack.
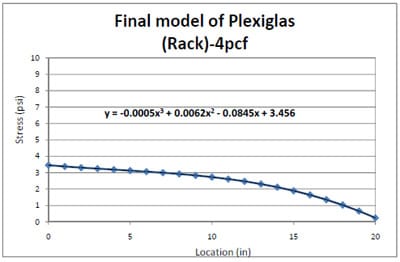
Figure 4.12 Final model of 4pcf foam stress distribution from the edge to the center of Plexiglas® deckboard.
4.3.1.4 6pcf Foam
6pcf foam stress distributions over a steel pallet deckboard are illustrated in Figure 4.13. This test results show that stresses are dramatically decreased along the deckboard from the edge to the center. Even with the steel deckboard in this test, the measurable images could not be traced around 13 to 27 inches in the deckboard location due to the high stiffness of the 6pcf foams and the steel pallet deckboard. Therefore, less than 2psi of stresses occurred in this area. 1psi was the most reasonable assumed value (between 0 to 2psi) and was therefore applied to the area between 13 and 27 inches.
This result exhibited a high level of load bridging. The level of load bridging can be determined from packaging style, pallet stiffness and storage type. Higher load bridging occurs when packaging with a rigid bottom, such as steel drums and cinder blocks, is supported by pallet stringers instead of a span of deckboards (Clarke, 2001). Hence, in this study, the rigid steel pallet deckboard and stiffer 6pcf foams resulted in the typical load bridging.
Based on stress distributions in Figure 4.13, a functional form of 6pcf foam stress distribution was generated and presented in Figure 4.14. Figure 4.15 shows 6pcf foam stress distributions across a Plexiglas® pallet deckboard in a simulated pallet storage rack. The results revealed that the stresses were much less transferred than those were shown in other foam results from a 280lb compressive load; however, 60% higher stresses were presented around the two outer stringers in 6pcf foam results than the 2pcf (Figure 4.7) and 4pcf foams (Figure 4.11) in the rack simulation. This result could also be explained by the load bridging principle. Figure 4.16 shows the final model of resultant 6pcf foam stress distributions. In Figure 4.16, the bold black line indicates the actual applied stress of 2psi, while the red line represents the estimated resultant final model. The final model includes negative stresses generated according to the functional form. In reality, however, the negative stresses are not predicted so they are discarded for FEA modeling.
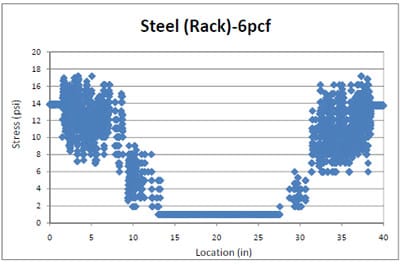
Figure 4.13 6pcf foam stress distribution across a steel pallet deckboard in simulated pallet rack storage.
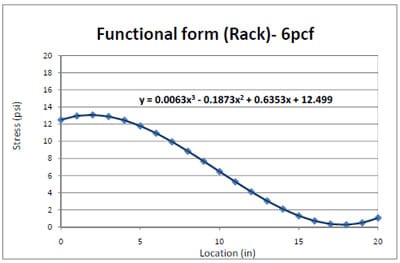
Figure 4.14 Functional form of 6pcf foam stress distribution from the edge to the center of a steel deckboard in simulated pallet storage rack.

Figure 4.15 6pcf foam stress distribution across Plexiglas® deckboard in simulated pallet storage rack.
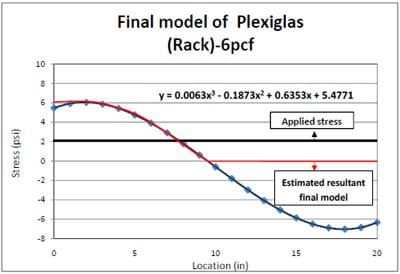
Figure 4.16 Final model of resultant 6pcf foam stress distribution from the edge to the center of a Plexiglas® deckboard.
4.3.1.5 Flour Sacks
For the testing, seven flour sacks were compressed with a 280lb load in the pallet storage rack condition. The stress distribution result of the flour packaging test was used to compare to the stress distribution of the three foams. Figure 4.17 shows the flour sack stress distribution across a Plexiglas® pallet deckboard in a simulated pallet storage rack. When comparing the results of the flour sacks and three foams, the flour sacks show higher stresses levels than any of the foams. However, the tendency of the flour sacks stress distributions was similar to that of the 2pcf and 4pcf foams. The stiffness of the flour sack was not tested; however, a comparison of stress distributions obtained from the three foams and flour sacks may determine which foam stiffness comes closest to that of the flour sacks.

Figure 4.17 Flour sacks stress distribution across a Plexiglas® deckboard in simulated pallet storage rack.
4.3.2 Simulation of Block Stack Storage Condition
4.3.2.1 Introduction
This section will compare the results obtained from three foams’s compressive static stress distributions over ½” and ¾” Plexiglas® deckboards in a simulated block stack storage system. A steel pallet section was used for the 4pcf and 6pcf foams to generate functional forms, due to the same complications that were encountered in the pallet storage rack simulation case. Testing of 2pcf foams produced enough measured data across a Plexiglas® deckboard to analyze stress distributions. The methods and procedures used for the analysis of results were the same as those used for the pallet storage rack simulation.
4.3.2.2 2pcf Foam
Figure 4.18 illustrates the 2pcf foam’s compressive static stress distributions across a ½” Plexiglas® deckboard in the simulated block stack storage. A 700lb (5psi) compression load resulted in non-uniform stress distributions over the pallet deck; stress concentrations occurred around three stringers. In the pallet storage rack simulation, the outer most stress levels from the test data for each of three stringers were spanned across the stringer areas (see Figure 4.18) instead of actual experiment data. In the block stack storage simulation, three stringers functioned as supports because the pallet was stacked on the floor.
Figure 4.19 shows a final model of resultant 2pcf foam stress distribution from the edge to the center of a ½” Plexiglas® deckboard in the block stack storage condition. The resultant final model predicted that the stress level at the center of the deck was slightly higher than at the edge, but the experimental data indicated little or no difference in stress levels at three stringer areas. This was because the third order equation was chosen as a model for the trend of stress distribution in the test data.
The 2pcf foam stress distribution across a ¾” Plexiglas® deckboard in the simulated block stack storage is shown in Figure 4.20. There was no difference in trends of stress distributions between ½” and ¾” deckboards. This means that over the ¾” Plexiglas® deckboard as well as the ½”, higher stresses were concentrated around three stringers. However, when comparing the variation of stress levels at each location along the deck, the ¾” deck had greater stress variation than the ½” deck. In addition to variation, the levels of distributed stresses around stringers over the ¾” deckboard were approximately 2 psi greater than over the ½” deckboard.
Figure 4.21 shows the final model of resultant 2pcf foam stress distribution, used for FEA modeling to predict a deflection of the ¾” Plexiglas® deckboard in the block stack storage condition. Overall stress levels distributed across a ¾” deckboard were higher than over a ½” deckboard in the resultant final model.
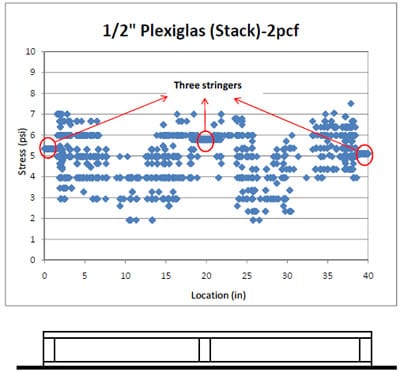
Figure 4.18 2pcf foam stress distribution across a ½” Plexiglas® pallet deckboard in simulated block stack storage.
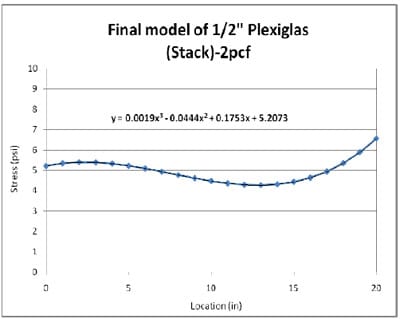
Figure 4.19 Final model of resultant 2pcf foam stress distribution from the edge to the center of ½” Plexiglas® deckboard.
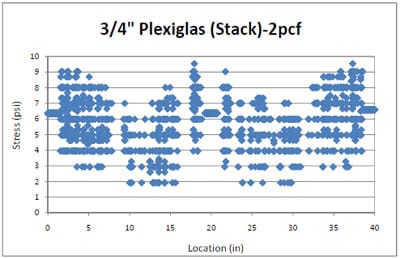
Figure 4.20 2pcf foam stress distribution across a ¾” Plexiglas® deckboard in simulated block stack storage.
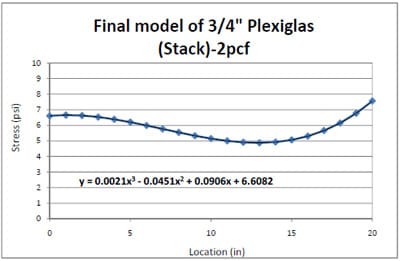
Figure 4.21 Final model of resultant 2pcf foam stress distribution from the edge to the center of ¾” Plexiglas® deckboard in simulated block stack storage.
4.3.2.3 4pcf Foam
Figure 4.22 shows the three replications of the 4pcf foam stress distributions over the steel pallet deckboard in simulated block stack storage. The trend of the 4pcf foam stress distributions was also similar to the distribution results obtained from the 2pcf foams. The functional form derived from the test data using the steel deckboard to predict the 4pcf foam stress distributions across Plexiglas® deckboards is shown in Figure 4.23.
The 4pcf foam stress distributions over ½” and ¾” Plexiglas® deckboards which are shown in Figure 4.24 and Figure 4.26, respectively. As the 2pcf case showed, the distributed stress levels for 4pcf foam were higher over the ¾” Plexiglas® deckboard than the ½” deck.
Figures 4.25 and 4.27 show the final model generated from the resultant 4pcf foam stress distributions from the edge to the center over ½” and ¾” Plexiglas® deckboard, respectively. The final models of resultant stress distributions over ½” and ¾” Plexiglas® pallet deckboards were predicted with different third equation forms, which were then applied to FEA modeling. The final model of resultant 4pcf foam stress distribution over a ¾” deck also shows more highly distributed stresses than the ½” deck.
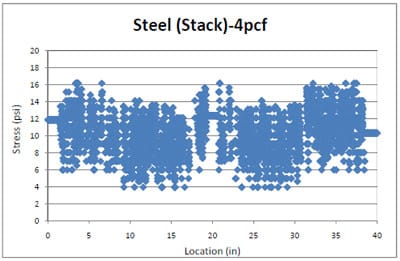
Figure 4.22 4pcf foam stress distribution across a steel deckboard in simulated block stack
storage.
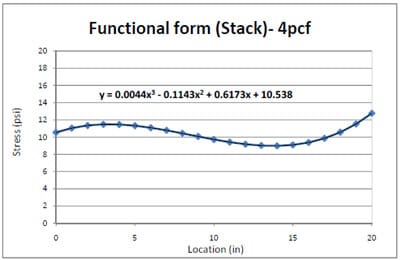
Figure 4.23 Functional form of resultant 4pcf foam stress distribution from the edge to the center of steel deckboard in simulated block stack storage.
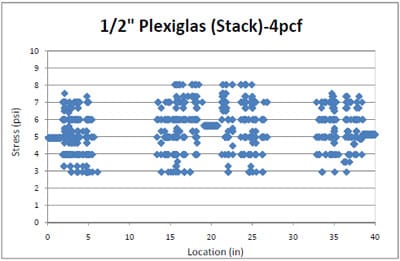
Figure 4.24 4pcf foam stress distribution across a ½” Plexiglas® deckboard in simulated block stack storage.
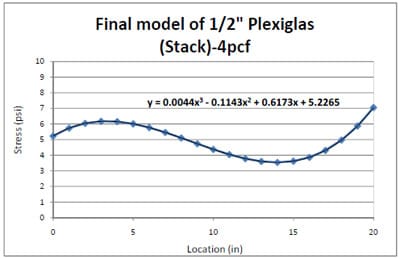
Figure 4.25 Final model of resultant 4pcf foam stress distribution from the edge to the center of ½” Plexiglas® deckboard in simulated block stack storage.
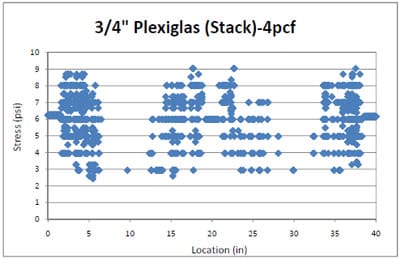
Figure 4.26 4pcf foam stress distribution across a ¾” Plexiglas® deckboard in simulated block stack storage.
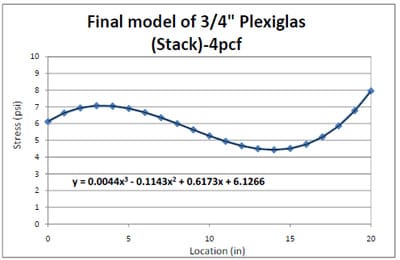
Figure 4.27 Final model of resultant 4pcf foam stress distribution from the edge to the center of ¾” Plexiglas® deckboard in simulated block stack storage.
4.3.2.4 6pcf Foam
As shown in Figure 4.28, the trend of 6pcf foam stress distribution over a steel pallet deckboard seems to be similar to the 4pcf foam stress distributions. However, the overall stress levels of 6pcf foam along the steel deck decreased slightly from those of 4pcf foam, as did the variation of stress levels along the steel deck. Figure 4.29 shows the functional form of resultant 6pcf foam stress distribution.
Figures 4.30 and 4.32 provides test data obtained from the 6pcf foam compression testing with a 700lb load over ½” and ¾” Plexiglas® deckboards, respectively. According to the results there were very few differences in stress levels and variation between the stress distributions over two different thicknesses of deckboards. Based on this result, it was concluded that 6pcf foam stress distribution was not influenced by the stiffness of the deckboard.
The resultant final models predicted by the functional form had little difference between ½” and ¾” deckboards, as shown in Figures 4.31 and 4.33.
4.3.2.5 Flour Sacks
Figures 4.34 and 4.35 present the results obtained from flour sacks compression testing over ½” and ¾” Plexiglas® deckboards, respectively, in simulated block stack storage. Trends, stress levels and variations in flour sack stress distributions over ½” and ¾” deckboards seem to be similar to the results of the 4pcf stress distribution over ½” and ¾” deckboards, respectively.
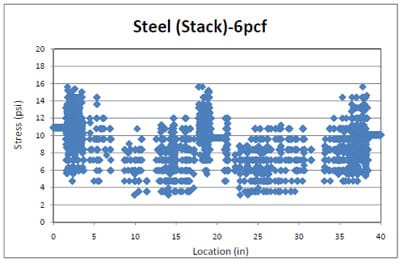
Figure 4.28 6pcf foam stress distribution across a steel deckboard in simulated block stack storage.
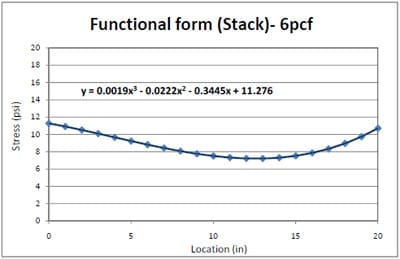
Figure 4.29 Functional form of resultant 6pcf foam stress distribution from the edge to the center of steel deckboard in simulated block stack storage.
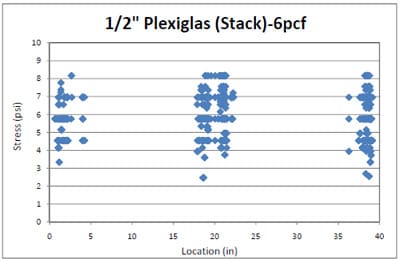
Figure 4.30 6pcf foam stress distribution across a ½” Plexiglas® deckboard in simulated block stack storage.
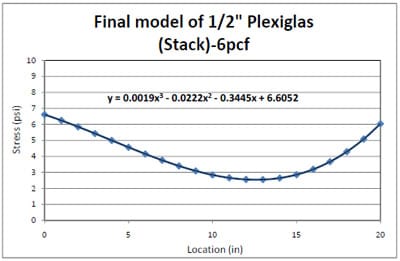
Figure 4.31 Final model of resultant 6pcf foam stress distribution from the edge to the center of ½” Plexiglas® deckboard in simulated block stack storage.
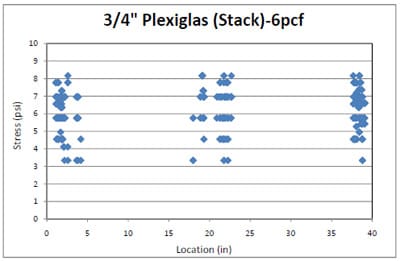
Figure 4.32 6pcf foam stress distribution across a ¾” Plexiglas® deckboard in simulated block stack storage.
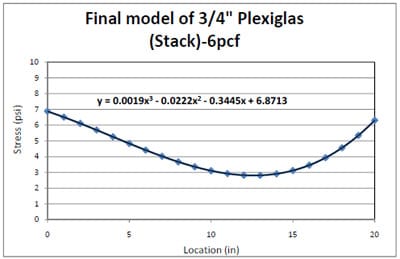
Figure 4.33 Final model of resultant 6pcf foam stress distribution from the edge to the center of ¾” Plexiglas® deckboard in simulated block stack storage.
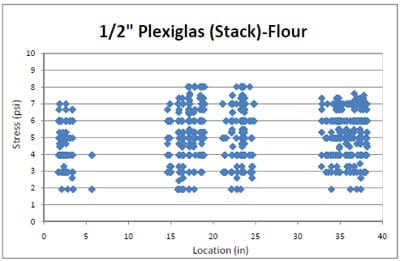
Figure 4.34 Flour sacks stress distribution across a ½” Plexiglas® deckboard in simulated block stack storage.
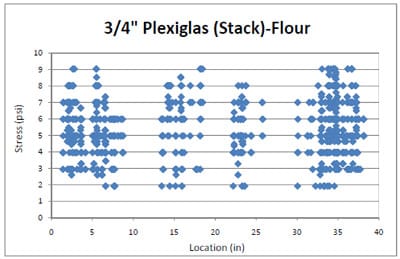
Figure 4.35 Flour sacks stress distribution across a ¾” Plexiglas® deckboard in simulated block stack storage.
4.3.3 Discussion
The wide range of stress level variance over the deckboards might have been caused due to the sensitivity of the corrugated fiberboard medium. Paperboard quality, environmental factors, and manufacturing tolerance can influence the medium condition. As the condition of the medium could be different for each testing, there may be differences in impressions left on the film. More importantly, the two faces (single face and double back) of the corrugated pad could be a critical factor. During testing, the crushed direction of the corrugated fiberboard pad was consistent. As seen in Figure 4.36, when the medium was crushed by compression, the contacted areas of the medium to double back face were wider than the single face. Thus, placing different faces on the bottom may have a significant effect on the width of the lines on the film images.
Figure 4.36 A schematic of crushed corrugated fiberboard medium after compression.
Figure 4.37 shows the final models of resultant three foams’ stress distributions in pallet storage rack simulation. As indicated in the final models, resultant compressive static stress distributions of the three foams were similar in their general tendencies, in which stresses around outer stringers were higher than the inner stringer. However, the three foams had some differences in the degree of change in stress concentrations, calculated by the ratio of maximum stress level to applied stress. As indicated in Figure 4.37, a bold black line shows the applied compressive stress of 2psi in a simulated pallet storage rack. The final model of resultant 2pcf foam stress distribution showed approximately 89% increased stress around the outer stringer compared to the applied stress level. Approximately 73% of the higher stresses were concentrated around the edge of deckboard than in the applied stress in the 4pcf foam final model of resultant stress distribution. In the final model of 6pcf foam stress distribution, the stress level was about 200% higher around the outer stringer than in the case of the applied stress of 2 psi. Greater stress concentrations occurred around the edge of the deckboard and more dramatic decreases in the stress levels along the deck were shown in the resultant 6pcf foam’s stress distribution than two other foams.

Figure 4.37 Final models of resultant three foams’stress distributions from the edge to the center of ¾” of Plexiglas deck in simulated pallet storage rack.
Figure 4.38 shows final models of resultant three foams’ stress distributions from the edge to the center of ½” and ¾” Plexiglas® deckboards in simulated block stack storage. The stress levels obtained from the 2pcf and 4pcf foams’ compression tests showed 15% to 27% increases over the ¾” deck relative to the ½” deck. This result explained why more measurable test data were generated over the ¾” deckboard than the ½” deck. The results of 6pcf foam stress distributions showed similar resultant final models between ½” and ¾” deckboards. From this, it is known that distributed stress levels across the deckboard shown in the 6pcf foam final model were not dependent on the deckboard thickness. The degree and location of stress concentrations along the pallet deck showed differences among the three foams. The final model of resultant 2pcf foam stress distribution over the ½” deck showed that the maximum stress concentrated around the inner stringer was a 31% increased stress relative to the applied stress of 5 psi in the simulated block stack storage. The resultant 2pcf foam final model of the ¾” deck showed that the maximum stress was 51% higher than 5 psi. In the final model of resultant 4pcf foam stress distributions over the ½” and the ¾”, respectively, 41% and 59% higher stresses than the applied stress occurred and concentrated around the inner stringer. The 6pcf foam final models of stress distribution showed the greatest change in stress levels along the deckboard, which means the stresses around the outer stringers were 218% to 248% higher than those in the center of the deck. The maximum stresses that occurred around the edge over the ½” and the ¾” were 32% and 37% higher, respectively, than the applied stress of 5 psi, as shown in the final model of resultant 6pcf foam stress distribution. Consequently, the stiffer foam caused greater change in stress levels along the pallet deckboard. In a block stack storage situation, the stiffness of foams has more significant effect on the change in stress distributions and concentrations along the deck than does the stiffness of deckboard.
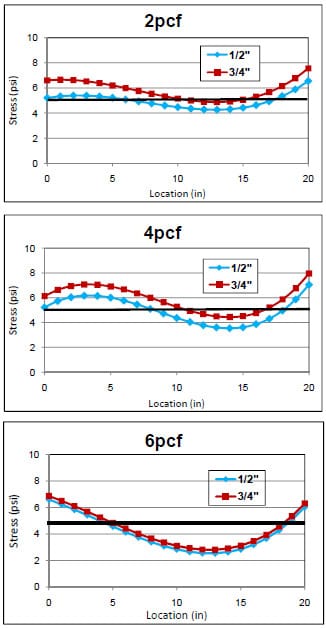
Note: ‘Bold black lines’ represent applied stress of 5psi for compression testing.
Figure 4.38 Final models of resultant stress distributions from the edge to the center of 1/2″ and 3/4″ Plexiglas deck in simulated block stack storage.
There were a few limitations found in this study. It was expected that the shapes of final models could vary depending on the pallet deck stiffness. However, the same functional form was fitted to ½” and ¾” Plexiglas® deckboards for each of 4pcf and 6pcf foams’ test data. The same functional form resulted in parallel final models of resultant stress distributions over ½” and ¾” deckboards for each of 4pcf and 6pcf foam as shown in Figure 4.38.
As illustrated in Figure 4.39, because of the difference in the stiffness of the foams, the rate of loading varied significantly, during testing using the same test machine rate of cross head movement 0.5 in/min. The estimated rate of loading was 9.5, 18.9, and 50.0lbs/sec for the tests using 2, 4, and 6pcf foams, respectively. The response of the corrugated medium and the pressure sensitive film may be influenced by the varied rate of test load application. The results shown in Figure 4.39 of the test conducted at different test machine cross head displacement rates indicates that increasing displacement rate reduces sensitivity to rate of loading. At the same load rate, for instance of 10lb/sec, the maximum stress was approximately 74% higher in 4pcf foams (12.43psi) than in 2pcf foams (7.14psi) and 172% higher in 6pcf foams (19.42psi). This means the maximum stresses will be higher than those shown in Figure 4.38 for 4pcf and 6pcf foams; however, this study did not control the rate of load during the testing. Although the maximum stress levels could be predicted from the results shown in Figure 4.39, changes in the shapes of the final models would still be unknown. To study the effect of the load rate on the changes of final model shapes, functional forms must be generated from the testing of each foam at the same load rate.
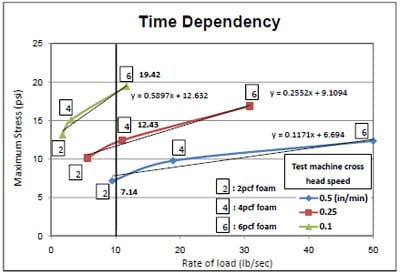
Figure 4.39 Time dependency of maximum stress for three foams
All test durations were less than 2 minutes. Compressive stress distributions might change during longer test cycle. For example, creep of the pallet deck and the corrugated medium may alter the compressive stresses during long-term storage. Therefore, in this study the resultant compressive stresses were assumed to be initial compressive stresses.
Table 4.2 shows adjusted initial maximum resultant compressive stress intensity factors after adjustment to the same 10 lbs/sec rate of load (Figure 4.39). The factors were calculated as the ratio of maximum resultant compressive stresses to the applied stresses. As seen in the table, the maximum compressive stress intensity factors were more significantly affected by the stiffness of foams than the stiffness of deckboards. These factors are useful to package designers who need to calculate the maximum compressive stresses which occurr during warehouse storage. Clearly, the design of the pallet can influence the level of compressive stress concentrations. An example how the stress intensity factors can be used in a real warehouse distribution environment for designing packaging is described below and in Figure 4.40.
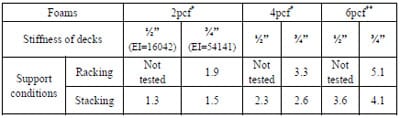
Table 4.2 Adjusted*** initial maximum resultant compressive stress intensity factors.
Note:
- *: Similar to non-rigid packaging (e.g. Flour sacks)
- **: Similar to rigid packaging (e.g. Steel drums)
- ***: Adjusted maximum resultant compressive stresses to rate of load (Figure 4.39)
Flour sack stress distributions in both pallet storage rack and block stack storage simulations were relatively similar to the 4pcf foam stress distributions. Therefore, it was concluded that the stiffness of the flour sack might be similar to that of the 4pcf foam stiffness.
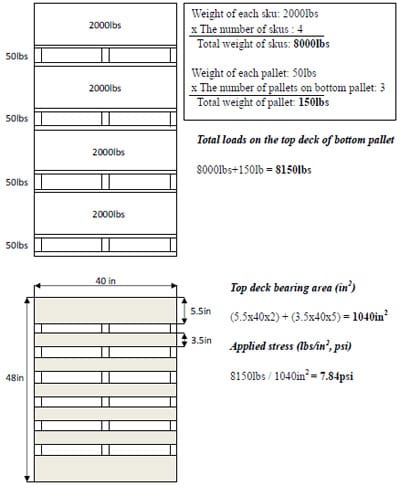
Figure 4.40 Example calculation of the maximum compressive stress at the pallet/package interface using maximum resultant compressive stress intensity factors from table 4.2
The final models of resultant stress distributions will allow packaging, pallet, and unit load designers to predict the degree of stress that occurs over specific locations in a pallet deck. Additionally, the resultant stress distributions will help packaging, pallet, and unit load designers to understand how package stiffness influences the stress concentrations along the deck, depending on the deckboard stiffness during warehouse storage.
4.4 Deflection
4.4.1 Simulated Pallet Storage Rack Condition
Figure 4.40 presents a comparison of deflections obtained from a 280lb compression load placed on 2pcf, 4pcf, and 6pcf foams compression load along a ¾” Plexiglas® deckboard in a simulated pallet storage rack condition. The deflections of the deckboard were measured at five locations: 0.75, 10.25, 20, 29.75, and 39.25 inches, for the three foam compression tests.
The results of the three foams’ compression testing presented a similar deflection tendency. The highest deckboard deflection occurred at 20 inches for all three foams. When comparing the degree of deflection among the three foams, the 2pcf foam compression resulted in the highest deflection and the 6pcf foam, had the least. The deckboard deflection showed an approximately 41% decrease in the 4pcf and an 82% decrease in the 6pcf relative to the 2pcf foam at the center of the deck where the maximum deflection occurred. Therefore, the stiffness of the foam had a significant effect on the deflection of a pallet deck in a pallet storage rack condition.
4.4.2 Simulated Block Stack Storage Condition
Figure 4.41 shows the trends and comparisons of ½” and ¾” Plexiglas® deckboard deflections. These tests measured deflection at five points and used the compression of three different foams in a simulated block stack storage condition. Figure 4.42 presents a comparison of maximum deflections obtained from three foam compression tests over ½” and ¾” Plexiglas® deckboards. For both ½” and ¾” deckboard, maximum defections were calculated by taking the mean of the deflections at 10.25 and 29.75 inches. In the case of the ½” deckboard deflections, the maximum deflection difference between 2pcf and 4pcf foams was less than 10%. The maximum deflection occurring in the 6pcf foam was decreased by about 66% over that of the 2pcf foam. The result obtained from the ¾” deckboard presents nearly the same deflection trend as the ½” deckboard results. The differences in maximum deflections between 2pcf and 4pcf foams were less than 4%, while the 6pcf foams shows about a 60% decrease relative to the 2pcf foam.
Figure 4.43 compares the ½” and ¾” Plexiglas® deckboard maximum deflections by the compression of three foams in simulated block stack storage. When comparing the deflection of the ½” deck to the ¾” deck to the compressed 2pcf foam, the results show that deflection decreased by approximately 50% in the ¾” deckboard. Similar to the 2pcf foam result, the compression load applied to the 4pcf and 6pcf foams over the ¾” deck decreased the deflections by 47% and 37%, respectively.
4.4.3 Discussion
The results of the deflection tests in both pallet storage rack and block stack storage system simulations demonstrated that the stiffness of the foams, which simulated the stiffness of packaging, had a considerable influence on the pallet deck deflections. In the simulated pallet storage rack condition, maximum deflection occurred at the 20 inch point. Greater differences in the deckboard deflections were observed in the simulated pallet storage rack than in the block stack storage condition. Therefore, the interaction between packaging with stiffness in the range of 2pcf and 4pcf foams and the pallet should be taken into greater consideration in the pallet storage rack than block stack storage system.
In this study, the different thicknesses of pallet decks represented different stiffnesses of the pallet deck. The differences in the deckboard deflections, caused by various stiffness of packaging, were dependant on the deckboard stiffness. Stiffer deckboard resulted in the greatest decrease in deflections with the 2pcf foam. The 2pcf foam simulated the most flexible and softest packaging. Using more stringers as well as a thicker deck will increase pallet stiffness. Another way to decrease deflection is to place more stringers between the deckboard components. These experimental deflection results are compared to predicted results from FEA modeling in the next section.
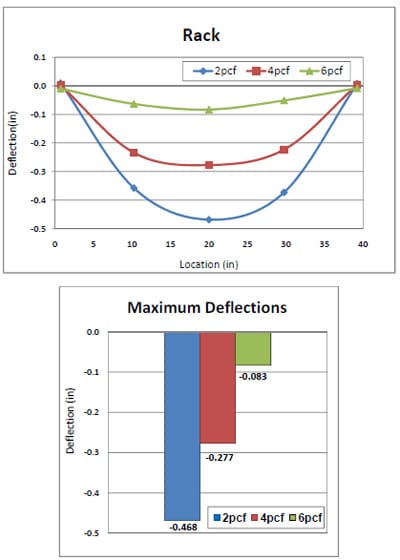
Note: Maximum deflections measured at the center of deckboard (20 inches) for three foams.
Figure 4.41 Comparison of ¾” Plexiglas® deckboard deflections and maximum deflections by three foams compression testing in simulated pallet storage rack.
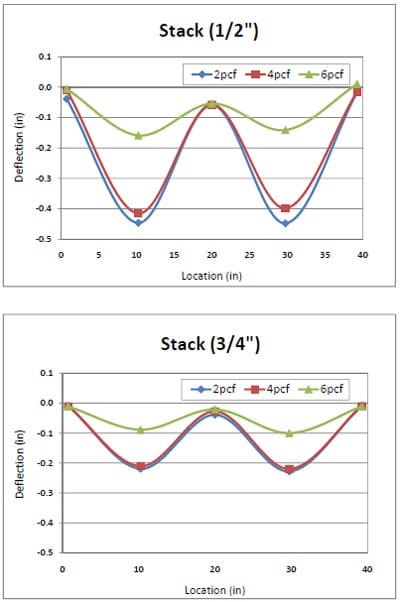
Figure 4.42 1/2″ and 3/4″ Plexiglas® deckboard deflections and maximum deflections by three foams compression testing in simulated block stack storage.
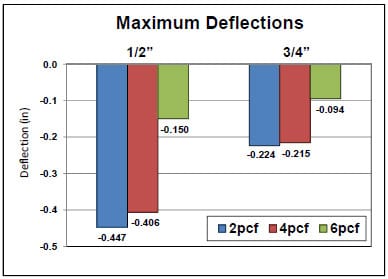
Figure 4.43 Comparison of maximum deflections obtained from three foam compression tests over ½” and ¾” Plexiglas® deckboard.
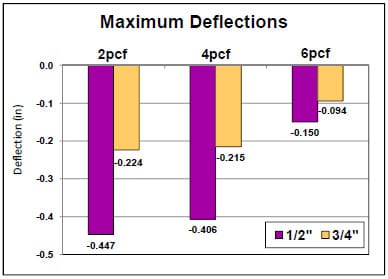
Note: Maximum deflections are the mean of deflections at 10.25 and 29.75 inches for three foams.
Figure 4.44 Comparison of ½” and ¾” Plexiglas® deckboard maximum deflections by compressed three foams in simulated block stack storage.
4.5 FEA Models of Pallet Deckboard Deflections
4.5.1 Simulated Pallet Storage Rack Condition
Figure 4.45 shows an FEA model of the predicted deflect
ion of a top pallet deckboard in a pallet storage rack simulation. A final model of resultant 2pcf stress distribution was applied to the modeling. The final model of resultant stress distribution is valid from the edge to the center for the left half. That half of the final model was mirrored so that the stress distribution could be defined for the other half of the top deckboard. FEA simulations for 4pcf and 6pcf foams were performed in the same way as the 2pcf.
A Table 4.2 presents a summary of the comparisons between the predicted deflections using FEA modeling and experimental deflections in the pallet storage rack condition for the three foams. The predicted maximum deflections for the three foams were in close agreement with the experimental maximum deflections, with differences of less than -10.8%. The differences of the maximum deflections for the 2pcf, 4pcf, and 6pcf foams between the predicted and the experimental results were -10.8%, -4.7%, and – 1.9%, respectively. The differences were calculated by the following formula:

4.5.2 Simulated Block Stack Storage Condition
Figure 4.46 shows an FEA model of a predicted ½” top deckboard deflection by the 2pcf foam compression in the block stack storage condition. As expected, the model shows minimum deflections around the three stringer areas due to the boundary conditions of 0 displacements enforced at the edge of the stringers. Maximum deflections occur around the midpoint between two stringers (left outer and inner stringer; right outer and inner stringer).
Tables 4.3 and 4.4 show, respectively, a summary of the predicted and the experimental deflection results of ½” and ¾” deckboards in the simulated block stack storage condition. The differences between the experimentally measured and the predicted maximum deflections for the three foams were evaluated by taking the difference of means of the deflections measured and predicted at 10.25 and 29.75 inches along the deckboard. The mean differences between the experimental and the predicted maximum deflections of ½” deckboard for the 2pcf, 4pcf, and 6pcf foams are -6%, 2.9%, and 28.6%. In comparisons between the predicted and the test maximum deflections of ¾” deckboard, the results from the 2pcf, 4pcf, and 6pcf showed differences of -15.4%, – 8.3%, and -26.7%.
4.5.3 Discussion
The predicted maximum deflections in the simulated pallet storage rack and the ½” deck in the block stack storage condition agreed closely with the experimental results. Although there were some differences between the simulation and the experiment results, the FEA models that predicted top deck deflections showed similar tendencies in the deflection results. These similarities were found in the location of maximum and minimum deflections, which occurred along the deckboard. The differences between the results are due to several possible reasons. During FEA modeling, only the top deckboard was modeled to simplify the simulation. However, the connection stiffness between stringers and decks may have significant effect on the deckboard deflections during the testing. Loose nails may allow the free movement and greater deflections of deckboard during the testing. Inaccurately defined properties of Plexiglas® used for a pallet deckboard material or element types may also create the errors or differences.
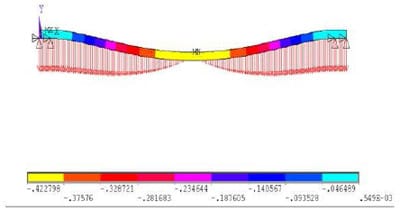
Note: ‘Red arrows’ represent the distributed stresses obtained from the final model of 2pcf foam stress distribution (Figure 4.7).
Figure 4.45 The predicted deflection for top deck by compressed 2pcf foams in pallet storage rack condition using FEA modeling.
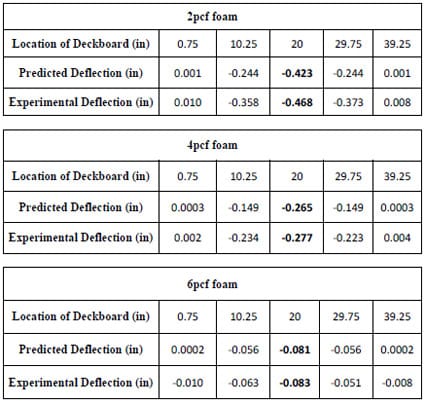
Table 4.3 Comparisons of predicted to experimental deflection for three foams in simulated pallet storage rack.
Notes:
- Experimental deflections are the mean of three replicates of testing.
- Values in “Bold” represent the maximum deflections at the center of top deckboard.
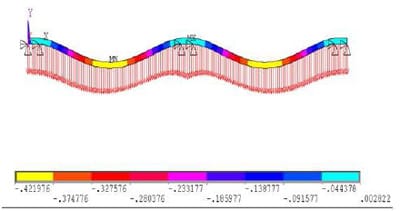
Figure 4.46 The predicted deflection for ½” top deck by compressed 2pcf foams in block stack storage condition using FEA modeling.
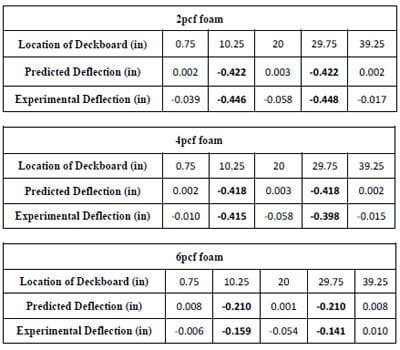
Table 4.4 Comparisons of predicted to experimental ½” deck deflection for three foams in simulated block stack storage.
Notes:
- Experimental deflections are the mean of three replicates of testing.
- Values in “Bold” represent the maximum deflections at 10.25 and 29.75 inches of top deckboard.
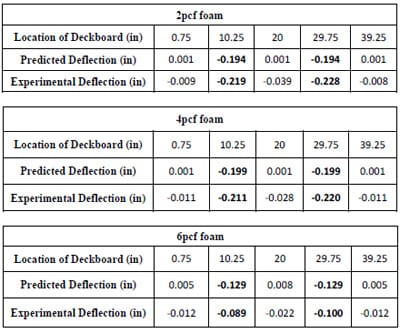
Table 4.5 Comparisons of predicted to experimental ¾” deck deflection for three foams in simulated block stack storage.
Notes:
- Experimental deflections are the mean of three replicates of testing.
- Values in “Bold” represent the maximum deflections at 10.25 and 29.75 inches of top deckboard.
CHAPTER 5 CONCLUSIONS AND RECOMMENDAITONS
5.1 Conclusions
- The compressive stress distributions between the simulated packaging and pallet deck were non-uniform in both simulated warehouse racking and floor stacking conditions.
- The measure of the stress concentrations was the stress intensity factor, which was the ratio of the adjusted initial maximum resultant compressive stress to the applied stress. Table below is a summary of the estimated initial compressive stress intensity factors as a function of foam stiffness (density) and pallet deck stiffness during simulated warehouse rack or stack storage.
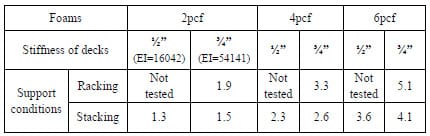
Table Conclusions #2 - The difference in the stiffness of the foams resulted in a significantly varied rate of loading during testing. The response of the corrugated medium and the pressure sensitive film were influenced by the varied rate of test load application. The stress intensity factors were adjusted to the same rate of loading.
- The stress intensity factors were affected more by the stiffness of the foam than the stiffness of the pallet deck.
- The warehouse rack storage simulation resulted in greater stress concentrations (stress intensity factors) than the floor stack storage simulation.
- Resultant adjusted initial maximum compressive stresses were 89% to 414% higher than the applied stress around the outer stringers during simulated rack storage and 31% to 311% higher than the applied stress around all three stringers in simulated floor stack storage. However, the compressive stresses are greater over the center st
ringer. - Preliminary tests indicated the 2pcf and 4pcf foams represented flexible packaging and sacked products and the 6pcf foam represented rigid packaging. There in little difference between the 2pcf and 4pcf foams in the levels of compressive stresses distributed along the pallet deck during both the simulated pallet storage rack and block stack storage conditions. The adjusted maximum compressive stresses between the pallet deck and the 6pcf foam was greater than 2pcf and 4pcf foams during both the warehouse storage simulations.
- The differences in deflection among the three foams were relatively large when compared with differences in maximum compressive stress. The deck deflections were less when compressing the stiffer foam. The maximum deck deflections occurred at the center of the deckboard in simulated warehouse rack storage, and at the deck location of 10.25 and 29.75 inches in the floor stacking condition.
- The stiffness of the pallet deckboard had an effect on the stress distributions and the pallet deck deflections in the block stack storage condition (the stiffness of the deck was not controlled in the pallet storage rack simulation). It was observed that 15% to 27% higher stresses are distributed over a ¾” (EI= 54140) deckboard than a ½” (EI= 16041) deckboard when the compression load was applied in the floor stack storage condition. The stiffer deckboard reduced deflection by approximately 37% to 50% during the floor stack storage.
- Predicted deckboard deflections developed by applying the resultant stress distributions to a 2-D FEA model of the pallet deck were validated by the comparison with experimental deflections. The agreement between predicted and measured deflections of a ¾” Plexiglas deckboard in pallet storage rack simulation is good, with a difference of less than 10%. In the block stacking condition of ½” and ¾” deckboards, the differences between measured and predicted deflection was 3% to 28.6%.
5.2 Recommendations for Future Study
I would recommend the following:
- A full size pallet should be tested instead of a pallet section to more realistically analyze the distributed stresses and deflections which occur during warehouse storage.
- The effect of joint connection stiffness on static stress distribution and deflections should be studied.
- Direct stress measurement is required, rather than indirect methods of measurement.
- Rate of load should be controlled during the testing.
- The image analysis technique can be improved by using a more sophisticated computer software program to obtain greater accuracy in the analysis of results.
- A pressure detector with greater/increased sensitivity should be used to detect pressure of less than 2psi.
- A greater variety of forms of real packaging should be considered for testing so that the methodology used in this research can be validated with more accurate results.
- FEA models of deflections should be considered regarding the influence of the joint connection method during modeling.
- Future study is required to develop a three-dimensional FEA model which is closer to a real pallet structure.
- Further study of foams or a packaging stiffness analog.
- Test needs to be conducted to monitor compressive stresses during long-term simulated storage.
References
Armstrong, W. R. Packaging supplies: Part 1 – Exterior packaging selection. Journal. Retrieved August 2, 2008 from https://www.sealedair.com/library/articles/packaging_supplies_pt1.html
ANSYS®. (2008). ANSYS ED 10.0 Retrieved August 13, 2008, from https://ansys.com/products/ed.asp
Bernie, K. (2005). How palletizers stack up. Modern Materials Handling, 60(6), 35.
Biancolini, M. E., & Brutti, C. (2003). Numerical and experimental investigation of the strength of corrugated board packages Packaging Technology and Science, 16(2), 47-60.
Bodig, J., & Jayne, B. A. (1993). Mechanics of wood and wood composities (Rev. ed.). Malabar, FA: Krieger publishing company.
Brebbia, C. A., Connor, J.J. (1974). Fundamentals of Finite Element Techniques. New York: Halsted Press.
Changfeng, G. (1996). Efficient Packaging Design in Logistics. Packaging Technology and Science, 9(5), 275-287.
Clancy, D. A. (1988). A New Package to Reduce Damage Claims. Transportation & Distribution, 29(12), 20.
Clarke, J. W. (2002a). Balance your pallet design. Pallet Enterprise, 91.
Clarke, J. W. (2002b). Cost, performance tradeoffs of racks, pallets. Pallet Enterprise, 87.
Clarke, J. W. (2002c). Europallets: good or bad for business? Pallet Enterprise, 89.
Cook, R. D. (1989). Concepts and Applications of Finite Element Analysis. New York: J. Wiley & Sons.
Connolly, L. (2000). Effect of loading and vibration on bending properties of pallet deckboards. Forest product journal, 52(9).
Corinne, K. (2007). Pallet rack basics. Modern Materials Handling, 62(2), 42.
Corrugated Packaging Alliance. History of Corrugated. Retrieved August 29, 2008, from https://www.corrugated.org/Basics/AboutCorrugated.aspx
Hamner, P., & White, M. S. (2005, November 1). Virginia Tech: How to design around a unit load. Pallet Enterprise.
Hamner, P., & White, M. S. (2006, May 6). Virginia Tech series: The next big idea- A case for systematic vs. Component unit load design. Pallet Enterprise.
Han, J., White, M.S., & Hamner, P. (2007). Development of a Finite Element Model of Pallet Deformation and Compressive Stresses on Packaging within Pallet Loads. Journal of applied packaging research, 1(3).
Hanlon, J. F., Kelsey, R. J., & Forcinio, H. E. (1998). Handbook of package engineering (3rd ed.). Boca Raton, FL: CRC Press LLC.
Haygreen, J. G., & Bowyer, J. L. (1996). Forest products and wood science: an introduction (3rd ed.). Ames, IA: Iowa state university press.
Huebner, K. H., Dewhirst, D. L., Smith, D. E. & Byrom, T. G. (1982). The Finite Element Method for Engineers: John Wiley & Sons, Inc.
Integrated Storage Solutions Inc. Storage and picking solutions. Retrieved August 2, 2008, from https://www.interlakerack.com/storagesolutions.html
Lee, S. M. (2008). Image analysis software program.
Lisa, M. K. (2005). Damaged Goods. Material Handling Management, 60(12), 16.
Mackes, K. H. (1998). Predicting the static bending behavior of pallets with panel decks. Unpublished Ph.D., Virginia Polytechnic Institute and State University, United States — Virginia.
Marshall White on the state of pallets. (2006). Modern Materials Handling, 61(3), 53.
Material Handling Industry of America. GMA pallet. Retrieved May 17, 2008, from https://www.mhia.org/learning/glossary/G
Monaghan, J., & Marcondes, J. (1992). Overhang and pallet gap effects on the performance of corrugated fiberboard boxes. Transactions of the Asae, 35(6), 1945-1947.
Robertson, G. L. (1993). Food packaging : principles and practice. New York Marcel Dekker, Inc.
Selke, S. E. M. (1994). Packaging and the environment (Rev. ed.). Lancaster, PA: Technomic publishing Company, Inc.
Twede, D., & Selke, S. E. M. (2005). Handbook of paper and wood packaging Technology. Lancaster, PA: DEStech Publications, Inc.
Urbanik, T. J. (1996). Machine Direction Strength Theory of Corrugated Fiberboard. Composites Technology & Research, 18(2), 80-88.
Weigel, T. G. (2001). Modeling the dynamic interactions between wood pallets and corrugated containers during resonance. Unpublished Ph.D., Virginia Polytechnic Institute and State University, United States — Virginia.
Weigel, T. G., & White, M. S. (1999). The effect of pallet connection stiffness, deck stiffness and static load level on the resonant response of pallet decks to vibration frequencies occuring in the distribution environment. Packagin
g Technology and Science, 12(2), 47-55.
Weigel, T. G. P.: Modeling the dynamic interactions between wood pallets and corrugated containers during resonance.
White, M. S. (2005). The effect of mechanical interactions between pallets and packaging on packaging costs. Preshipment testing newsletter(4), 18,20,22.
White, M. S. (2007). Systems based design Retrieved August 28, 2008, from https://www.whiteandcompany.net/systems-based.htm
White, M. S., & Hamner, P. (2004). Topographical mapping of the mechanical stresses on wood pallets during use. Virginia Tech.
White, M. S., & Hamner, P. (2005). Pallets move the world: the case for developing system-based designs for unit loads. Forest product journal, 55(3), 8-16.
White, M. S., Rupert, R. L., & Clarke, J. W. (2006). Basic corrugated packaging and unit load design short course, Virginia Tech, Blacksburg, VA.
White, M. S., Rupert, R. L., & Clarke, J. W. (2006). Unit load design short course, Virginia Tech, Blacksburg, VA.
Appendix:
Material properties of Plexiglas® , CELLUPLANK®, and Calibration data
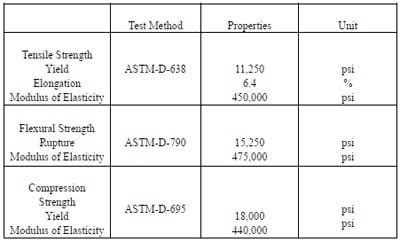
table Appendix A. Physical properties of Plexiglas®.
*Data were provided by SPARTECH POLYCAST Co.
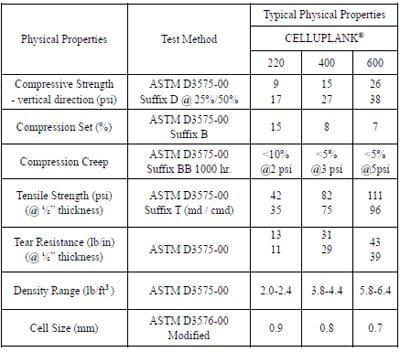
table Appendix B: Physical properties of CELLUPLANK®.
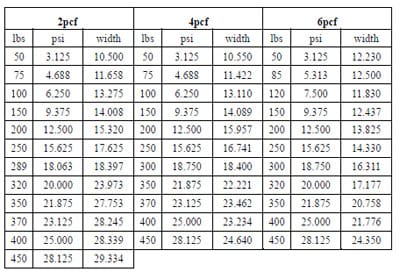
Appendix C: Load levels used for calibration of pressure sensitive film (*psi was calculated by each load (lbs) divided by 16 in2, which is from dimension of foam used for applying loads).