Investigation of the through-plane impedance technique for evaluation of anisotropy of proton conducting polymer membranes

Tatyana Soboleva ^a, Zhong Xie ^b,*, Zhiqing Shi ^b, Emily Tsang ^a, Titichai Navessin^b, Steven Holdcroft ^a,b,*

^aDepartment of Chemistry, Simon Fraser University, 8888 University Drive, Burnaby BC, Canada V5A 1S6

^bInstitute for Fuel Cell Innovation, National Research Council Canada, 4250 Wesbrook, Mall Vancouver BC, Canada V6T 1W5

Abstract
Two-probe electrochemical cells were designed for proton conductivity evaluation in the X, Y and Z directions using electrochemical impedance spectroscopy (EIS). Nafion^® 112, 115, 1135, 117 and 211 membranes were used to examine the conductivity in the three given directions, and to determine the influence of cell configuration and probe geometry on the accuracy and reproducibility of the measurement. Emphasis is placed on obtaining an understanding of the real system and adequate transfer of the physical processes into the form of the equivalent circuit for the extraction of reliable conductivity data. In order to verify that the method can determine anisotropic conductivity, novel fluorous block copolymers with various anisotropic phase segregated morphologies were evaluated. All polymer electrolyte membranes examined exhibited a Nyquist plot response in the form of a straight line with an angle of approximately 70°–80° to the Z’-axis. Interfacial capacitance, membrane bulk resistance and membrane bulk capacitance were considered as contributing parameters to the impedance of the system; high frequency inductance and contact resistance were instrumentally minimized. A marginally anisotropic conductivity (σ=/σ_┴ = 1.0–1.4) was found in all Nafion^® samples. Fluorous block copolymers with disordered morphology exhibited higher conductivity in the through-plane direction by a factor of 1.4. For the polymers with perforated lamellae and lamellae morphologies, in-plane conductivities were larger by factors of 2.4 and 5.5, respectively.

1. Introduction
Proton conductivity is a crucial criterion for evaluating fuel cell performance as well as the practicability of novel PEM materials. Commonly, proton conductivity is measured along the plane of the membrane [1–3]. However, in practice, the membrane requires proton conduction perpendicular to the membrane. Relying only on in-plane conductivity values could lead to inaccuracies in estimating the membrane performance especially in the case of materials exhibiting morphological anisotropy. This fact increases the importance of implementing the through-plane conductivity technique in studies of fuel cell membranes.

There are several reports in the literature on the anisotropic morphology of Nafion and the expectation that anisotropic proton conductivity is dependent on the membrane casting method and membrane pre-treatment procedure, e.g., hot-pressing [4–10]. Studies of novel polymer materials for fuel cell applications such as sulfonated polyimides show distinct morphological anisotropy [11,12] and anisotropic proton conductivity.

There are few reports [4,5,7,10,13–22] on the application of the ex situ through-plane impedance technique for ion conducting membranes using various methodology and apparatus for the through-plane conductivity measurement. A through-plane measurement has been described by Ma et al. and consisted of two Pt sheets coated on one face using 5 lL of 5% Nafion dispersion [7]. Nafion membranes were sandwiched between two electrodes and hot-pressed. The corresponding 4-probe arrangement was prepared by sandwiching and hot-pressing two polyester-coated wire electrodes between three Nafion membranes. In another example, Pt microelectrodes were placed in contact with both sides of a Nafion sample [13]. An electrochemical cell comprising of a Nafion membrane sandwiched between two carbon paper electrodes was used by Ramya et al. [19]. A cell equipped with mercury electrodes was used by Blachot et al. [12] to measure ionic conductivity of sulfonated polyimide membranes. A 2-probe stainless steel electrochemical cell was used to measure ionic conductivity of alkaline membranes by Wu et al. [14,17] and Yang [16]. A cell comprising of graphite current collectors, carbon paper electrodes was used by Silva et al. [21]. Nafion membranes were inserted between two carbon paper porous disks and were hot-pressed in a similar way as that of membrane-electrode assemblies. In these experiments, the applied frequency ranged from 0.01 Hz to 5 MHz, and in most cases a response in the form of a straight line inclined to the Z’-axis in the Nyquist plot was reported. However, detailed information about the cell configuration and the data extraction methods are sparse, yet they are crucial to the unambiguous interpretation of impedance spectra.

It is generally believed that the in-plane conductivity measurements are easier to carry out and provide greater accuracy due to the larger cell constant, L/A, where L is the distance between electrodes, usually several millimeters, and A is the cross-sectional area of the sample. Thus, the main contribution to the measured impedance comes from the bulk membrane, and other interfering resistances are negligibly small. However, in the through-plane arrangement, the cell constant is small, since L corresponds to the membrane thickness, in the range of micrometers, and A is the area of the electrodes, which is generally much larger. Thus, the impedance contributions from the interfacial region between the polymer membrane and the electrodes are more important.

In this paper, a simple 2-probe electrochemical cell consisting of 2 Pt electrodes that sandwiches the membrane is used to measure through-plane proton conductivity of a series of Nafion membranes (Z-direction). Emphasis is placed on understanding the physical processes in the system and the meaningful construction of the equivalent circuit that allows for the reliable extraction of conductivity data. A 2-probe in-plane conductivity cell is used to evaluate proton conductivity in 2 planar directions (X and Y directions). Model membranes based on block copolymers of sulfonated poly([vinylidene difluoride-co-hexafluoropropylene]-b-styrene, comprising of a nonionic fluorous block and a sulfonated ionic block (see Scheme 1), and exhibiting well-defined phase separation and anisotropy are evaluated to elucidate the sensitivity of the technique to the morphological anisotropy [23]. Samples possessing disordered, perforated lamellar and lamellar morphologies are used in this
work.

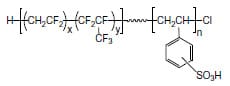
Scheme 1. Structure of the flourous-block-ionic diblock copolymer.

2. Experimental
2.1. Materials
Nafion 112, 115, 117 and 1135 membranes from DuPont were pretreated with 3% H₂O₂, deionized water and 2 M HCl aqueous solution at 100 °C for 30 min and stored in water. Nafion 211 membrane samples were soaked in deionized water for 24 h prior to use. The IEC for all Nafion membranes is 0.91 mmol/g according to specifications. Hydrated thicknesses are 60, 158, 216, 105 and 28 μm for Nafion 112, 115, 117, 1135 and 211, respectively.

Partially sulfonated poly([vinylidene diflouride-co-hexafluoropropylene]- b-styrene) block copolymers were synthesized by Shi et al. A detailed procedure of this synthesis is described elsewhere [24,25]. Copolymers with different contents of the polystyrene segment and with different degrees of sulfonation were prepared by dissolving received copolymer samples in THF solvent (P99%) and casting on a Teflon sheet. Samples were allowed to dry in air for 2 h, and under vacuum for 24 h. The copolymer consisting of 10 wt% polystyrene sample (1) possessed a disordered morphology; the 30 wt% polystyrene sample (2) phase segregated into a perforated lamellar morphology; and the sample consisting of 25 wt% of the polystyrene ionic block (3) possessed a lamellar morphology. The films possessed thicknesses ranging between 35 and 100 lm. Membranes were immersed into 2 M HCl and deionized water for 24 h, respectively, washed, and stored in deionized water. The IECs for the samples (1), (2) and (3) are 1.20 mmol/g, 0.89 mmol/g and 0.69 mmol/g, respectively. The cross-sectional TEM micrographs of these membranes, together with a representative Nafion membrane are shown in Fig. 1. The method for acquiring these TEMs has been reported extensively elsewhere [24,25]. The dark regions represent ionic domains.

Fig. 1. TEM micrographs of (a) Nafion and fluorous block copolymers:
(b) disordered morphology, (c) perforated lamellae morphology and (d) lamellae morphology.

2.2. Instrumentation and electrochemical cells
Impedance measurements were performed using a Solartron impedance analyzer SI 1260 in the frequency range from 10 MHz to 100 Hz and 100 mV amplitude. Z plot/Z view software package was used to set measurement parameters and to analyze data.

The through-plane conductivity cell was constructed from two PTFE blocks and Pt sheets (0.1 mm thick) as illustrated in Fig. 2a. Pt sheets were attached to the PTFE blocks to create the electrode area. The PTFE blocks were held together by two nylon screws. Pt electrodes were connected to the Solartron impedance analyzer by means of pins. Prior to conducting the measurements, the cell was calibrated to determine the high frequency inductance of the cell by measuring impedance of the shorted cell, and of the ‘‘opened” cell. Both data files were saved and subsequently used as nulling files in Z plot software. Membranes were cut into ~5 x 5mm samples for the through-plane impedance measurement. The sample was sandwiched between two Pt electrodes, and the cell was tightened with screws. Compression pressure applied on the membrane was estimated using Pressurex^® pressure indicating films sensitive to the range of pressures between 350 psi and 1400 psi (film type ‘‘low”). The cell was immersed in deionized water at 20 °C and impedance data was collected.

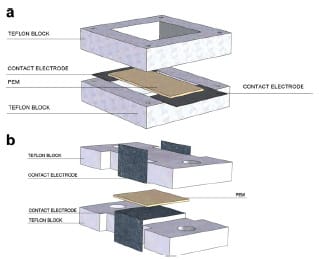
Fig. 2. (a) In-plane and (b) through-plane impedance cells showing the probe arrangement.

Two PTFE blocks and Pt sheets 0.1 mm thick were used to construct the in-plane conductivity cell. Two Pt sheets 10 x 10 mm were attached to one of the PTFE blocks – the distance between them was 5 mm, Fig. 2b. PTFE blocks were connected by means of nylon screws. Membranes were cut into ~10 x 10 mm pieces and placed between electrodes. The entire setup was placed in deionized water at 20 °C. Impedance was measured in two perpendicular in-plane directions, the X and Y directions.

In both cases, conductivity was calculated:

σ = L ÷ (R • A’)         (1)

where L corresponds to the electrode separation: the gap between electrodes for in-plane measurements and the thickness of the polymer film for through-plane measurements. A is the membrane cross-sectional area in case of the in-plane setup and the area of the electrodes in case of the through-plane setup. R is the bulk membrane resistance.

3. Results and discussion
3.1. Equivalent circuit diagram
Interpretation and quantification of the impedance spectrum requires understanding of the processes occurring and an appropriate equivalent electric circuit model. However, in practice the simplicity of the model is as important as its adequate reflection of the real system. Therefore, it is necessary to understand the physical processes in the cell and to identify the main components contributing into the overall impedance of the system in order to determine an accurate representation in the form of an equivalent circuit. In the through-plane assembly, by placing the proton conducting polymer film between two Pt electrodes, a blocking electrode/electrolyte interface is created. An idealized circuit for such a system can be represented by the equivalent electric circuit shown in Fig. 3a. Each membrane/electrode interface is represented by a parallel combination of a capacitance, corresponding to the capacitance of the double layers, C_int1 and C_int2, and a resistance, that models the resistance of the blocking interfaces, R_int1 and R_int2. The impedance of the polymer electrolyte film constitutes the bulk resistance, R_b, in parallel with the bulk membrane capacitance, C_b. The impedance of the cell hardware is not included in the circuit since the cell is calibrated by shorting before usage and the impedance of the electrodes is automatically subtracted from the measured value, as described in the Section 2.

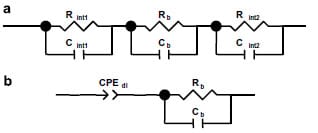
Fig. 3. Equivalent circuits for the proton conducting membrane sandwiched
between two electrodes. (a) Idealized circuit: R_int1, R_int2 and C_int1, C_int2 represent the
impedances of the membrane-electrode interfaces; R_bulk and C_bulk represent the bulk
membrane resistance and capacitance, respectively. (b) Simplified equivalent
circuit used to fit the experimental data.

Since Faradaic charge cannot cross the interface, the behavior of the electrode/electrolyte interface is merely capacitive [15,26–29] and resistances R_int1 and R_int2 can be omitted from the circuit. The double layer capacitance, in turn, has two parts in series: the Helmholtz compact layer capacitance and the diffuse double layer capacitance. The former is a weakly varying function of applied potential, usually in the range of several μF. The latter varies exponentially with potential but for the measurements using small potential differences its contribution to the overall capacitance is negligibly small [15,26]. Thus, the dominant process at the proton conducting medium/blocking electrode interface can be represented by the double layer capacitance of the Helmholtz layer.

An ideal capacitive behavior would result in the vertical linear line in the Z’ vs. Z” diagram. However, it is generally recognized that capacitance at solid electrodes deviates from ideal behavior in the form of a phase-angle frequency dependency. This capacitive dispersion is due to irregularities of the electrode surface, expressed as so-called fractal geometry [28]. Thus the interfacial impedance can be described by a constant phase element (CPE):

Z(w) = 1 / (iwC_dl)^n’        (2)

where, C_dl is independent of w, and ½ < n < 1 (if n = 1, Eq. (2) becomes the impedance of a pure capacitor)[15]. The real part is resistive and the imaginary part is capacitive, both proportional to w½. Interfacial resistance arising with the formation of the double layer by protons traveling to/from the interface is negligible small at high frequencies (w >>1/(R x C)) [27] since the distance they need to travel is in the range of several Ångstroms (thickness of the Helmholtz compact layer), which is insignificantly small compared to the thickness of the polymer film, which is in the range of 30–160 lm. Thus, the through-plane impedance can be expressed in terms of the electric circuit elements as shown in Fig. 3b, where CPE_dl represents interfacial capacitance; R_b in parallel with C_b are the bulk resistance and bulk capacitance of the membrane, respectively.

According to the equivalent circuit (Fig. 3b), the impedance can be expressed as:

Z(w) = ((1 / R_b) + (iwC_b)^-1) – (1 /(iwC_dl)ⁿ        (3)

and the impedance spectra are expected to comprise of a semicircle in the high frequency region, corresponding to the bulk membrane impedance, and an inclined spur in the low frequency region, corresponding to interfacial capacitance [30].

3.2. Instrumental mitigation of the interfering factors
3.2.1. Eliminating the contact resistance
Further examination of the experimental arrangement raises the question of the quality of the contact between the electrodes and the polymer membrane, and its effect on the overall impedance. There are two scenarios in which the contact region significantly impacts the measured impedance of the system. Since all used membranes are fully hydrated and the measurements are conducted in deionized water, it is possible that a thin layer of water is present at the region of contact. This could lead to an overestimation of the bulk resistance of the polymer film. Another possible source of inaccuracy may arise if the membrane’s morphology is different at the region of contact than in the bulk. Although accounting for these factors in the equivalent circuit seems reasonable, it increases the inaccuracy of experimental fitting since the magnitude of these features is difficult to estimate and is an unknown function of clamping pressure and the geometry of the probe. Based on these considerations, the equivalent circuit shown in Fig. 3b is used for the all through-plane impedance data fitting, and interfacial impedances are minimized instrumentally. The effect of improving the quality of the contact by increasing the cell compression is shown in Fig. 4a. Experimentally, the impedance response shifts to the left on the real axis with increasing compression, and converges to a common value, beyond which no further shift is observed upon further compression.

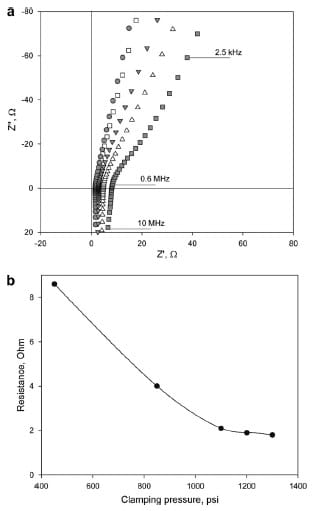
Fig. 4. (a) Through-plane impedance responses of Nafion 115 under different
clamping pressures, Nyquist plots. (○) 450 psi, (▼) 850 psi, (∆) 1100 psi, (■)
1200 psi, (●) 1300 psi and (b) Effect of increasing clamping pressure on measured
resistance of Nafion 115.

The filled squares in Fig. 4a represent the initial through-plane impedance spectra and filled circles correspond to the converged impedance plot, obtained at a clamping pressure of ~1300 psi. Furthermore, an increase of the angle of inclination of the linear portion of the spectrum from 55° to 70° is observed. An angle of 70°– 80° is characteristic of double layer formation at a rough electrode interface. This observation suggests that under pressure the roughness of the membrane/electrode contact decreases. It is important to note that no change in membrane thickness was observed after conducting measurements under given clamping pressures. A plot of measured resistance under estimated clamping pressure is shown in Fig. 4b. It is seen that for a clamping pressure of ≥1200 psi the resistance is relatively constant and minimal.

3.2.2. Correction for high frequency inductance
Inductance is one of the interfering factors in the through-plane impedance measurement. It usually appears in the fourth quadrant of the Nyquist plot in the high frequency region and in the most cases it is caused by external wiring that connects the potentiostat to the cell and by the electrodes themselves. Inductance is strongly related to the length and nature of the connecting wires; the shorter the wire length, the smaller the effect of inductance. Since the value of the membrane resistance is extracted from the high frequency region of the spectra, it is necessary to account and eliminate the contribution by inductance. This can be readily done by calibrating the cell by shorting, as described in experimental section. Impedance responses of a Nafion 115 membrane are shown in the Fig. 5, before (filled squares) and after (open squares) subtracting the cell inductance contribution.

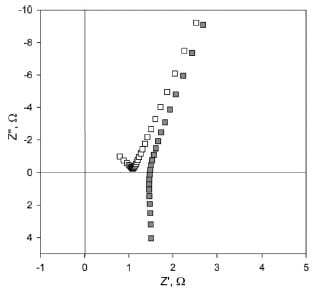
Fig. 5. Through-plane impedance response of Nafion 115 before (■)
and after (□) correcting for inductances.

3.3. Interpretation of the through-plane impedance spectrum
The polymer electrolyte membranes examined in this work exhibited an impedance response characterized by a straight line with an angle of 70°–80° to the Z’-axis in the range of frequencies between 1 MHz and 100 Hz. This is believed to be typical of the formation of double layer capacitance at a blocking electrode/electrolyte interface [26]. The onset of the semicircle observed in Fig. 5 at frequencies approaching 1 MHz is attributed to the impedance of the polymer electrolyte membrane to the conduction of protons.

3.3.1. Characteristic peak frequency
Resolution of the semicircle depends on the characteristic peak frequency, w_p, of the given system, which in turn is a function of the dielectric relaxation time of the material. The characteristic peak frequency is calculated as follows:

w_p = 1 / (R_bC_{b)        (4)}

where R_b is bulk resistance of polymer membrane and C_b is bulk capacitance. R_bC_b is the time constant (t) or the dielectric relaxation time of the material. If the time constant is sufficiently small that it satisfies the condition w_maxt<<1, little or none of the semicircle can be observed in the Nyquist plot. The peak frequency of a complete semicircle satisfies w_pt = 1; and only when w_maxt>>1 is the full semicircle obtained [30]. In the case of Nafion membranes, it is expected that the dielectric relaxation time is very low and thus higher frequencies are required to completely resolve the semicircle; often, as in this case, these higher frequencies cannot be attained with typical electrochemical frequency response analyzers. In order to verify that the arc observed in Fig. 5 truly represents the onset of a semicircle, and hence is due to the bulk membrane material, the impedance plot was fit in the equivalent circuit shown in Fig. 3b; the experimental and fitted data are shown in Fig. 6.

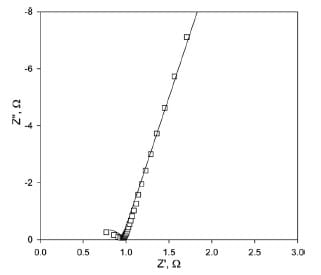
Fig. 6. Nyquist plot for Nafion 115 (–) fitting and (■) experimental data.

R_b for Nafion 115 obtained from the fitting is 0.97 (±0.01)Ω and the bulk capacitance is 7.0 (±0.5) x 10^-9 F. The frequency-dependent constant phase element (CPE) comprises of two elements: CPE-T, that models double layer capacitance at the membrane/ electrode interface, corresponding to Cdl in Eq. (2); and CPE-P, that is related to the roughness of the membrane-electrode contact represented by n in Eq. (2). The value of n varies between 1 for a very smooth surface and 0.5 for a highly rough surface. Numerical values for these parameters obtained from fitting are 3.79 (±0.03) x 10^-6 F for CPE-T and 0.933 (±0.006) for CPE-P.

The parameters obtained from the fit were then used to simulate impedance responses over more broader range of frequencies, i.e., much higher than experimentally attained. Nyquist plots for these simulations obtained for frequencies in the range of 100 Hz to 10 MHz, 20 MHz, 100 MHz and 1 GHz are shown in Fig. 7. As it is seen from the simulation, the semicircle passes through the coordinates’ origin and thus its diameter can be accepted as the membrane resistance as it is commonly accepted for in-plane conductivity measurements. From these spectra, the characteristic peak frequency for Nafion 115 membrane is ~20 MHz. The simulated Nyquist plot over the experimentally assessable frequency range, showing only the partial semicircle, is in good agreement with the experimental data, as illustrated in Fig. 6. Theoretical determination of the characteristic peak frequency requires the estimation of the bulk capacitance based on the information about the dielectric constant of the Nafion membrane:

C_b = εε₀ (A_PEM / L)        (5)

where A_PEM is the area of the PEM sample; L is the distance between electrodes (thickness of the membrane); ε₀ is the permittivity of free space, and has the value 8.854 x 10¹² F m^-1; ε is the dielectric constant for fully hydrated (λ = 22) Nafion membrane, and is ~32. This value was obtained by extrapolating the data for dielectric constants at different hydration levels as reported by Paddison et al. [31], and for which, the value of Cb is calculated to be 5.3 x 10^-11 F. Accordingly, the PEM characteristic peak frequency should be in the range of 5–10 GHz. However, simulation of the impedance spectra using parameters extracted from experimental data, yield a peak frequency of ~20 MHz, which implies the actual Cb is in the range of 1 x 10^-8 F. This finding leads to the conclusion that the membrane bulk capacitance is determined by the interplay of the additional processes besides the dielectric relaxation of the basic polymer material. This increase in bulk membrane capacitance might be due to polarization of water inside of the nano-sized pores and in close proximity to the sulfonic groups; and possibly from the interaction of the protons with the negative charges on the sulfonic groups.

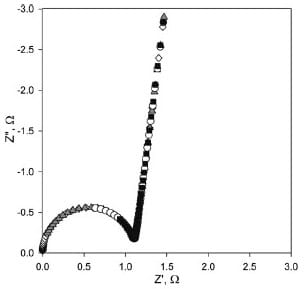
Fig. 7. Simulation Nyquist plots using the equivalent circuit shown in Fig. 3b and
parameters obtained from experiment at frequency range from (■) 100 Hz to
10 MHz, (○) 100 Hz to 20 MHz, (▲) 100 Hz to 100 MHz and (◊) 100 Hz to
1 GHz. Parameters: CPE-T = 3.79 x 10^-6 F, CPE-P = 0.933, R_b = 0.97 Ω and C_b
= 7.00 x 10^-9 F.

3.4. Data extraction
Many studies describe the evaluation of through-plane membrane resistance by simply taking a linear extrapolation of the impedance spike in the Nyquist plot to the Z0-axis and by accepting the intercept as the R_{b</ sub> value [11,12,14,16,17]. A more accurate method is to use the diameter of the semicircle; but, unfortunately, complete semicircles are not usually attainable. In this section, conductivity data extracted from impedance plots by two methods are compared. The first method involves simple extrapolation; the second – fitting of the impedance data to the equivalent circuit shown in Fig. 3b. For Nafion 117, the value of the membrane resistance assessed by linear extrapolation was 1.21 Ω; from an equivalent circuit analysis, a value of 1.18 Ω was obtained, i.e., a <3% deviation. For Nafion 112 the values were 0.45 Ω and 0.50 Ω for linear extrapolation and fitting, respectively, i.e., a 10% deviation. It is important to note that fitting errors for the Rb value for Nafion 117 and Nafion 112 are 1.2% and 2.0%, respectively.}

Table 1 shows a summary of the data for measured throughplane resistance and the calculated conductivity for Nafion 115 before and after correction for (a) contact resistance, (b) inductance, as well as a comparison of the two data extraction methods.

Table 1 Measured resistance and calculated conductivity values of Nafion
115 before and after mitigation of interfering effects

In summary, various correction factors should be considered when obtaining reliable through-plane conductivity data. The effects of these corrections can be summarized in the following manner: a cursory through-plane impedance measurement of Nafion 115 yielded a through-plane resistance (by extrapolation to the Z’-axis) of 8 X (this will vary with initial clamping pressure, electrode area, polymer thickness); increasing the clamping pressure reduced this to 1.80 Ω; after correcting for inductance the extrapolated resistance was reduced to 1.00 Ω; and by fitting the impedance plot to the equivalent circuit, the value was 0.97 Ω.

3.5. Anisotropic–isotropic proton conductivity
The impedance of various Nafion membranes (112, 1135, 115, 117, 211) was measured in the plane of the sample in two perpendicular directions, X and Y. Through-plane impedance was measured in a 0.29 cm² cell. Nyquist plots similar to that shown in Fig. 6 were obtained in all cases (Fig. 8a) and membrane bulk resistance values were extracted by analyzing the spectra in the context of equivalent circuit. Fitting errors for all membranes were under 6%.

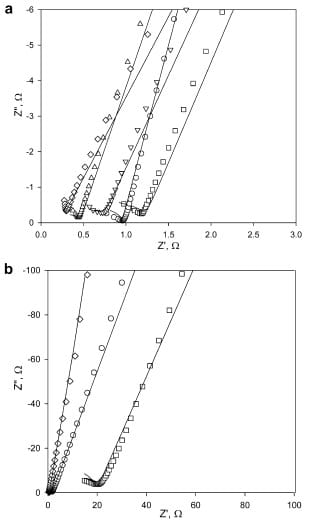
Fig. 8. (a) Experimental through-plane impedance spectra for (□) Nafion 117, (o)
Nafion 115, (∆) Nafion 112, (۷) Nafion 1135, (◊) Nafion 211 and corresponding fits
(–) and (b) experimental through-plane impedance spectra for fluorous block
copolymers: (□) lamellae, (o) perforated lamellae, (◊) disordered morphologies
and corresponding fits (–).

XYZ-conductivity data and the degree of anisotropy, expressed as the ratio of the in-plane to the through-plane conductivity, are presented in Table 2. All samples demonstrate isotropic proton conductivity in the two (X,Y) in-plane directions. A small degree of anisotropy in the through-plane direction was observed for all Nafion samples with the exception of Nafion 211. The highest degree of anisotropy is observed for Nafion 112, with the through-plane conductivity ~30% lower than the in-plane. The morphology of Nafion is still a subject of much research interest but its microstructure and nanostructure depend strongly on the method of membrane preparation. It is reported that membranes drawn perpendicular or parallel to the extruding direction demonstrate relatively anisotropic morphology, whereas quite isotropic morphologies are obtained when the membranes are processed with a simultaneous biaxial draw [6]. Anisotropic proton conductivity of Nafion 117 was reported by Gardner et al. [4,5]: through-plane conductivity (0.024 S/cm) was found to be ~70% lower than in-plane conductivity (0.086 S/cm). Two alternative explanations were provided to justify the observed results. Authors ascribed conductance anisotropy to the orientation of ionic clusters at the interface; and the orientation of the Nafion chains along the direction of membrane extrusion.

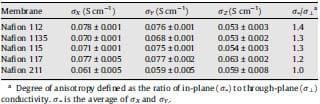
Table 2 In-plane and through-plane conductivity of Nafion membranes
and the degree of anisotropy

The reverse trend in anisotropy was presented by Yamada et al. [9]: through-plane conductivity for the Nafion 112 was reported to reach an atypically high value of 0.37 S/cm at 90 °C and 100% RH; 0.13 S/cm was reported for in-plane conductivity at 50 °C. Isotropic conductivities for Nafion 117, 115 and 112 were reported by Silva et al., however, conductivity values were lower than observed in this work, e.g., 0.048 S/cm for Nafion 117, 0.033 S/cm for Nafion 115 and 0.023 S/cm for Nafion 112 [21].

Our results point to a marginally anisotropic proton conductance and hence a slightly anisotropic phase separated morphology. Overall, this finding is consistent with information on the manufacture of Nafion. As expected, anisotropic morphology was found in the extruded membranes (Nafion 112, 115, 117 and 1135). However, isotropic conducting behavior was found in Nafion 211 that is a solution-cast membrane where no particular orientation of the polymer chains or conducting clusters is expected. Further morphological analysis would be helpful to explain the reason why extruded Nafion membranes differ in the degree of anisotropy from each other. Dependence of the through-plane membrane conductivity on thickness was also reported in [22] where the authors ascribe this behavior to variation of temperature and pressure during the extrusion of the membranes of different thicknesses. However, the purpose of this paper is to demonstrate the analytical methodology for obtaining conductivity data rather than understanding the morphological nuances of particular membranes, which requires additional methods of materials characterization.

Finally, we investigate three different fluorous block copolymers, each with similar composition, but each with a distinct morphology: disordered, perforated lamellae, and lamellae, as determined previously [24,25], representing increased anisotropy of the ionic, phase segregated domains. Previous studies indicate that the perforated lamellae and lamellae lie parallel to the membranes surface, as a result of their being cast from solution [24,32]. The impedance spectra for these three copolymers are shown in Fig. 8b. Conductivity in the X, Y, a
nd Z directions is presented in Table 3. Similar to Nafion, isotropic proton conductivity in two inplane (X, Y) directions was observed.

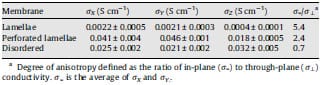
Table 3 In-plane and through-plane conductivity of fluorous block
copolymers possessing different morphologies

The deviation in through-plane conductivity values obtained by simple extrapolation versus fitting of the impedance data to the equivalent circuit was more significant for the fluorous block copolymer membranes. For the block copolymer membrane (3), linear extrapolation yields a membrane resistance of 17.8 Ω, whereas fitting with an equivalent circuit yielded a value of 22.4 Ω, a 21% deviation. Similarly, for the perforated lamellae sample (2), extrapolated and fitted values deviate from each other by 20%, 1.70 Ω and 2.13 Ω, respectively. For the morphologically disordered sample (1), the deviation was significantly lower ~2.2%.

For the purpose of obtaining the most accurate through-plane conductivity data, we used fitted impedance plots. Comparison of in-plane and through-plane data for the three fluorous block copolymer membranes revealed an anisotropy in conductivity consistent with the ionic anisotropy visualized by TEM. The in-plane to through-plane anisotropy increased from 0.7 to 2.4 to 5.4, for disordered (1), perforated lamellae (2) and lamellae morphologies (3), respectively. Fluorous membrane (1) was more conductive in the through plane direction for reasons that are not understood, but are being explored. For the lamellae membrane (3), the in-plane conductivity exceeds the through-plane by factor of 5.4. This suggests that the hydrophilic proton conducting layers are oriented along the plane of the membrane in such a way that hydrophilic and hydrophobic layers are marginally parallel to the membrane’s surface, which is consistent with the visualized lamellar morphology. As expected, anisotropy of the perforated lamellar (2), which can also be described as a slightly disordered lamellae morphology, lies between (1) and (2).

4. Conclusions
A two-probe electrochemical cell was used to evaluate the through-plane conductivity of polymer electrolyte membranes. It was found that main parameters contributing to the electrochemical impedance are membrane bulk resistance, bulk capacitance and interfacial double layer capacitance. Through-plane impedance spectra were found to be distorted significantly by contact resistance and inductance. However, these can be minimized instrumentally and through calibration. The impedance of the bulk membrane was extracted by fitting the impedance spectra using an equivalent circuit. This method was found to provide more reproducible and accurate data than simply extrapolating the low frequency line to the Z’-axis.

A study of the proton conductivity of various Nafion membranes demonstrated a slight anisotropy with the in-plane conductivity over the through-plane conductivity with the exception of Nafion 211. Novel fluorous solid polymer electrolytes possessing three different distinct morphology types showed anisotropic proton conductivity properties that were consistent with the visualized anisotropy of the ionic domains, and provided further confirmation of the reliability of the methodology for determining through-plane conductivity.

Acknowledgements
The authors thank Dr. Michael Eikerling for discussions on EIS. We would also like to thank the Machine Shop at Simon Fraser University for their assistance in manufacturing the conductivity cells.

References

1. T.A. Zawodzinski, M. Neeman, L.O. Sillerud, S. Gottesfeld, J. Phys. Chem. 95 (1991) 6040.
2. J.J. Fontanella, M.G. McLin, M.C. Wintersgill, J.P. Calame, S.G. Greenbaum, Solid State Ion. 66 (1993) 1.
3. T.A. Zawodzinski, C. Derouin, S. Radzinski, R.J. Sherman, V.T. Smith, T.E. Springer, S. Gottesfeld, J. Electrochem. Soc. 140 (1993) 1041.
4. C.L. Gardner, A.V. Anantaraman, J. Electroanal. Chem. 395 (1995) 67.
5. C.L. Gardner, A.V. Anantaraman, J. Electroanal. Chem. 449 (1998) 209.
6. K.A. Mauritz, R.B. Moore, Chem. Rev. 104 (2004) 4535.
7. S. Ma, Z. Siroma, H. Tanaka, J. Electrochem. Soc. 153 (2006) A2274.
8. K.M. Cable, K.A. Maurtiz, R.B. Moore, Chem. Mater. 7 (1995) 1601.
9. O. Yamada, Y. Yin, K. Tanaka, H. Kita, K. Okamoto, Electrochim. Acta 50 (2005) 2655.
10. Y.A. Elabd, C.W. Walker, F.L. Beyer, J. Membr. Sci. 231 (2004) 181.
11. W. Essafi, G. Gebel, R. Mercier, Macromolecules 37 (2004) 431.
12. J.F. Blachot, O. Diat, J.L. Putaux, A.L. Rollet, L. Rubatat, C. Vallois, M. Muller, G. Gebel, J. Membr. Sci. 214 (2003) 31.
13. A. Parthasarathy, B. Dave, S. Srinivasan, A.J. Appleby, C.R. Martin, J. Electrochem. Soc. 139 (1992) 1634.
14. G.M. Wu, S.J. Lin, C.C. Yang, J. Membr. Sci. 284 (2006) 120.
15. J.C. Wang, Electrochim. Acta 38 (1993) 2111.
16. C.C. Yang, S.J. Lin, J. Power Sources 112 (2002) 497.
17. G.M. Wu, S.J. Lin, C.C. Yang, J. Membr. Sci. 275 (2006) 127.
18. M.C. Wintersgill, J.J. Fontanella, Electrochim. Acta 43 (1998) 1533.
19. K. Ramya, G. Velayutham, C.K. Subramaniam, N. Rajalakshmi, K.S. Dhathathreyan, J. Power Sources 160 (2006) 10.
20. V. Tricoli, N. Carretta, M. Bartolozzi, J. Electrochem. Soc. 147 (2000) 1286.
21. R.F. Silva, A. De Francesco, A. Pozio, J. Power Sources 134 (2004) 18.
22. S. Slade, S.A. Campbell, T.R. Ralph, F.C. Walsh, J. Electrochem. Soc. 149 (2002) A1556.
23. Y. Yang, S. Holdcroft, Fuel Cell 5 (2005) 171.
24. Z.Q. Shi, S. Holdcroft, Macromolecules 38 (2005) 4193.
25. Z.Q. Shi, S. Holdcroft, Macromolecules 37 (2004) 2084.
26. A. Karthikeyan, P. Vinatier, A. Levasseur, Bull. Mater. Sci. 23 (2000) 179.
27. A.H.C.H. Hamann, W. Vielstich, Electrochemistry, Wiley VCH, 1998.
28. E. Barsoukov, Impedance Spectroscopy: Theory, Experiment, and Applications, Wiley-Interscience, 2005.
29. A.J. Bard, L.R. Faulkner, Electrochemical Methods: Fundamentals and Applications, John Wiley & Sons, 2001.
30. J.R. Macdonald, Impedance Spectroscopy: Emphasizing Solid Materials and Systems, John Wiley & Sons, 1987.
31. S.J. Paddison, D.W. Reagor, T.A. Zawodzinski, J. Electroanal. Chem. 459 (1998) 91.
32. E.M.W. Tsang, Z. Shi, T. Soboleva, S.Holdcroft, J. Am. Chem. Soc. 129 (2007) 15106.