Vishalini Bundhoo, Edmund Haslam, Benjamin Birch and Edward J. Park*
Department of Mechanical Engineering, University of Victoria, PO Box 3055 STN CSC, Victoria, British Columbia, Canada, V8W 3P6
Summary
Keywords: Artificial finger; Biomimetic design; Tendondriven mechanism; Shape memory alloy.
1. Introduction
In this paper, a new biomimetic tendon-driven actuation system for prosthetic and wearable robotic hand applications is presented. It is based on the combination of compliant tendon cables and one-way shape memory alloy (SMA) wires that form a set of agonist–antagonist artificial muscle pairs for the required flexion/extension or abduction/adduction of the finger joints. The performance of the proposed actuation system is demonstrated using a 4 degree-of-freedom (three active and one passive) artificial finger testbed, also developed based on a biomimetic design approach. A microcontroller-based pulse-width-modulated proportionalderivation (PWM-PD) feedback controller and a minimum jerk trajectory feedforward controller are implemented and tested in an ad hoc fashion to evaluate the performance of the finger system in emulating natural joint motions. Part II describes the dynamic modeling of the above nonlinear system, and the model-based controller design.
Rehabilitation robotics1-4 has grown significantly in the last two decades. Rehabilitation robotics is a special branch of robotics that aims at building robotic devices as a way to rehabilitate, assist, replace, or enhance impaired human motor control capabilities. This field includes a wide variety of systems ranging in complexity, from simple adaptive tools to advanced microcontroller-driven mechanisms, such as upper-limb myoelectric prostheses and lower-limb powered orthoses.
However, although tremendous technological progress has been made in the state-of-the-art of orthoses and prostheses, current devices cannot yet perform as well as their biological counterparts.5 In order to find a solution to this problem, engineers and scientists are turning to nature for inspiration and guidance. Nowadays, more researchers are focused on not only at building mechanical systems that will aid the disabled, but strive toward the development of biomimetic (i.e., lifelike) systems having the same adaptability, functionality, and cognitive abilities as biological systems. The trend in reverse engineering of nature is justified by the fact that, with millions of years of evolution, biological systems have evolved into very efficient and effective mechanisms. It is believed that imitating these systems represent enormous potential to improve the tools that we use. The continued advances in human–machine interfaces, muscle-like actuators, artificial sensors, and biomimetic control schemes promise to lead us to more sophisticated human-like artificial devices in the next several decades.6 As these biomimetic devices become more affordable, lighter in weight, and their ability to autonomously aid human motor functions increases due to the advances in the above component technologies, the range of applications in theworld of physical therapy, orthotics, and prosthetics will increase exponentially.
In the field of industrial robotics, significant advancements have already been made in terms of actuation transmission mechanism design, sensing, and control in the development of multifingered dexterous hands: e.g., the Belgrade/USC Hand, Stanford/JPL Hand, and Utah/MIT Hand.7-8 Some of the more recent developments include the NTU Hand,9 DLR Hand,10 NASA’s Robonaut Hand,11 and the commercially available Shadow Hand (from Shadow Robot Company). However, the problem of building similar hand devices for rehabilitation robotics differs considerably from the industrial robotics context, where the industrial hands typically operate in a structured environment with predefined tasks and, often, with no considerations to the human–hand interaction.12 Successful rehabilitation robots cannot be realized with direct application of only industrial robotic technologies; and rehabilitation robotics has many technical as well as nontechnical challenges.3 The following issues become more sensitive in rehabilitation robotics: (i) low cost, (ii) low weight, (iii) noiseless actuation, (iv) anthropomorphic size and appearance, (v) user safety, (vi) human–machine interface; hence, any device or component technology developed needs to be geared toward solving these issues. In addition, future rehabilitation robotics needs to be more human-friendly, i.e., not only on cosmetic alone but in function as well. Rehabilitation robots should be highly intelligent systems that would recognize the physical and cognitive abilities of the users so as to provide a higher level of comfort and functionality.4 For instance, it is a known fact that in the prosthetic hand field, commercially available devices (e.g., the OttoBock Sensor Hand or the Vasi Hand) have faced high user rejection rates owing to the rigidity of the artificial hands, their low grasping stability, heavy weight, the noisy operation of actuators, as well as the unnatural feel and robot-likemotion of the fingers.
In this paper, we present a biomimetic tendon-driven actuation system for artificial fingers employed in rehabilitation robots, particularly useful to wearable robotics (e.g., robotic exoskeletons and orthoses) and prosthetics. The proposed actuation system, which uses shape memory alloy (SMA) artificial muscles in a spring-biased agonist–antagonist (i.e., differential-type13 which is made of two opposing SMA elements) configuration, is demonstrated on a 4 degree-offreedom (DOF) biomimetic artificial finger testbed. The testbed itself is anthropomorphically and kinematically accurate physical model of the natural hand. Note that the above industrial dexterous hands mostly utilize the conventional electric or pneumatic actuation methods. However, the more strict considerations on size, appearance, weight, noise, and cost requirements14 of prosthetic or rehabilitation devices hamper the free use of conventional actuators that are bulky and noisy, and the use of complex motion transmission mechanisms. In an effort to improve the actuation system, a number of promising “artificial muscle” actuators that exhibit life-likemuscle behaviors have appeared, most notably McKibbon pneumatic artificial muscles15 and SMA artificial muscles. This paper is focused on the latter type, which have been successfully implemented in many biomedical applications.16
In the literature, SMA muscle wires have been proposed as actuators for a number dexterous hand and finger design, including the Hitachi Hand.17 This is another industrial robotic hand—a four-fingered (three fingers and a thumb) that utilizes multiple 0.02mm and 0.035mm diameterSMA wires to actuate its finger and wrist, respectively. De Laurentis and Mavroidis18 proposed a combined use of SMA wires and tendon cables for dexterous prosthetic hand applications, focusing on the mechanical design and fabrication of a finger using the selective laser sintering (SLS) rapid prototyping technique to facilitate the routing of the cables through it (the cables are then to be crimped to differential-type SMA wires in the palm). Very recently, Price et al.19 proposed a three-fingered SMA-based prosthetic hand, with bias-type SMA wires (i.e., composed of an SMA element and a bias spring) directly routed through the finger joints in a traversing arrangement. The main advantage of SMAs is that they can be used in direct-drive configuration eliminating the need for complex transmission systems. Furthermore, they possess a high power to weight ratio enabling the design of compact, lightweight systems without too much compromising power capabilities. Moreover, SMAs only use the phase transformation for actuation which permits silent operation. However, actuation rates are dependent on the cooling capacity of the wire which limits the actuator bandwidth. Other limitations are: limited life cycle, nonlinear operation owing to hysteretic behavior and still low actuation strains. The pros and cons of using SMAs for prosthetics are summarized in Kyberd et al.14 — who suggest that, due to the comparably low actuation bandwidth and forces, they could be more appropriate for a child’s prosthesis than an adult’s.
In order to design the proposed biomimetic tendon-driven actuation system, and the artificial finger testbed for the subsequent performance evaluation, the natural finger and its physiology—the muscle and tendon architecture and the sensory abilities—were studied and mimicked in a practically efficient manner. A novel contribution of this paper is the integration of a compliant tendon (via a springslack element) to each one-way SMA muscle wires. This allows the formation of true three agonist–antagonist (or differential) artificial muscle pairs for the actuation of the flexion/extension and abduction/adduction of the metacarpophalangeal (MCP) joint and the flexion/extension of the proximal interphalangeal (PIP) joint of the artificial finger. As a result, the proposed actuation system produces similar manipulative and functional abilities found in the natural finger. Tactile feedback is provided by the use of a simple resistive force sensor placed on the fingertip surface, while joint position feedback is obtained by embedding miniature potentiometers and a resistive bend sensor into the finger joints. A combined pulse-width-modulated proportionalderivation (PWM-PD) feedback controller and minimum jerk trajectory feedforward controller are implemented for each active joint via on-board microcontrollers to enable closedloop biomimetic control of the artificial finger. The resulting system is a low-cost, lightweight, stand-alone system suitable for ambulatory applications in rehabilitation robotics.
2. Human Finger Physiology
This section describes the key features of the human finger anatomy that we have considered to design an artificial finger that can be characterized as biomimetic.
2.1. Bones and joints of the human finger
The fingers of the human hand consist of three intercalated bony segments: the proximal, middle, and the distal phalanges. The proximal phalange is located at the base of the finger, connected to the metarcarpal bones in the palm of the hand, while the distal phalange is located at the fingertip. The finger joints are the MCP, the PIP, and DIP (distal interphalangeal) joints. Fig. 1 illustrates the location of the finger joints and phalanx. The MCP joint of the hand can be considered as a 2 DOF universal joint that allows for adduction/abduction and flexion/extension. The PIP and DIP joints are both single DOF revolute joints that are only capable of extension and flexion. However, the PIP and DIP joints are interdependent, i.e. the DIP is a passive DOF that is driven by the rotation at the PIP. Hence, the natural finger can be considered as a 4 DOF mechanism with three active and one passive joints.
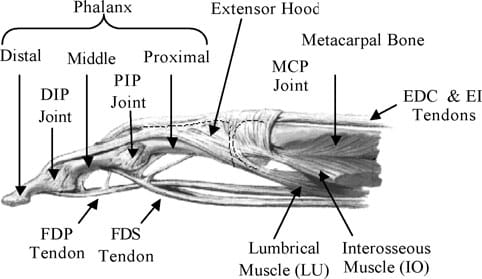
Fig. 1. Anatomy of the index finger.
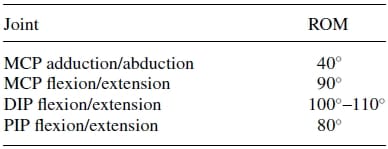
Table 1. Range of motion (ROM) of index finger23.
The range of motion (ROM) at the joints varies from finger to finger. Although the joint surface geometry defines the joint ROM, the effective range is also limited by the tendon network and ligaments of the fingers. The typical ROMof the index finger,which has the greatest range of extension/flexion amongst the fingers, is shown in Table I.
2.2. Muscles and tendons of the human finger
The tendons of the natural finger are collagen-based with nonlinear stiffness characteristics. Since the tendons get stiffer as they are stretched, they allow finger joints to flex or extend within a limited range. They also permit the finger to return to its original position after flexion/extension or abduction/adduction. The dynamic and highly redundant nature of the tendon structure renders the finger-actuating anatomy complex and difficult to fully comprehend and model. As such, only the tendons essential for the index finger flexion/extension and abduction/adduction are studied and mimicked in our design.
The muscles of the natural finger can be categorized into two groups: (i) extrinsic muscles, which are heavy lifting muscles located in the forearm, and (ii) intrinsic muscles, which are weaker muscles originating from the palm and used for precision movements of the fingers. Finger flexion is produced by the action of two extrinsic flexors: flexor digitorum superficialis (FDS), flexor digitorum profundus (FDP). The FDS tendon attaches the base of the middle phalanx, while the FDP attaches to the distal phalanx as shown in Fig. 1. Finger extension occurs through the action of a web-like structure referred to as the extensor hood that rides on the dorsal surface of the finger. Two main extrinsic extensors are the extensor digitorum (EDC) and extensor indicis (EI). The EDC and EI tendons merge with the extensor hood at the MCP. Beyond the hood, the EDC and EI separate into three bands: the central band that inserts dorsally at the base of the middle phalanx and the two lateral bands that rejoin as a terminal tendon at the base of the distal phalanx. Besides the above extrinsic flexors and extensors, three intrinsic muscles are necessary for finger motion. These are the lumbricals (LU), the dorsal and the palmar interosseous (IOs). The attachment of the LU and IOs are also shown in Fig. 1. The two IOs are connected to the sides of the proximal phalange. They work in opposition and control the adduction and abduction motions of the finger.
2.3. Finger senses
Besides its primary prehensile and manipulative functions, each finger also acts as a sense organ. The finger senses can be grouped into internal and external senses. The external finger senses, or tactile senses, refer to the tiny receptors embedded in the skin that capture and relay sensations of contact, pain, and temperature to the brain through the central nervous system.20 The internal senses, or proprioceptive senses, refer to receptors that are found within the human body, attached to joints, tendons, and muscles. The proprioceptors enable humans to perceive body movements, position and orientation in space, as well as assessing the external force the human body is subjected to, when muscles and joints undergo movements.21
3. Design of Biomimetic Artificial Finger Testbed
The design of a biomimetic artificial finger requires a profound understanding of the biological features of the human hand. However, the essential design goal is to accurately represent the important biological functions of the natural finger. In this work, the degree of emulation was limited to the following key factors, which were deemed essential characteristics of a biomimetic artificial finger: (i) anthropomorphically accurate size and appearance; (ii) kinematically accurate motion, (iii) tendon-driven agonist–antagonist biomimetic actuation, and (iv) biomimetic sensory feedback. Our key design constraints were to achieve these characteristic in a cost-effective and lightweight manner for rehabilitation robotic applications (e.g., prosthetics/orthotics or wearable exoskeletons). This section describes our biomimetic design philosophy behind the design of the artificial finger testbed, which is used to test the proposed tendon-driven actuation mechanism.
3.1. Anthropomorphically accurate size and appearance
Firstly, an anthropometric size was desired as our design goal was to maintain the physical attributes of the natural finger, while matching it functionality at the same time. Data pertaining to hand dimensions are available from Buccholz et al.22, where finger anthropomorphic data was conveniently expressed in terms of statistically derived coefficients that enabled for phalangeal lengths, phalangeal breadths/depths, and joint centers to be estimated from data on hand length, hand breadth, and bone length, respectively. The resulting dimensional values are summarized in Tables II, III, and IV. The artificial finger was designed within the boundaries of the physical dimensions given in the above tables to closely resemble the contours of the natural finger. Figures 2(a) and 2(b) are the CAD representations of the resulting artificial finger design, which is anthropomorphically consistent with the natural finger.
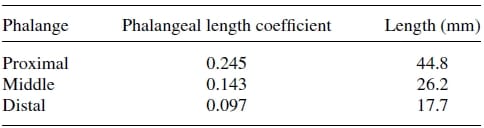
Table 2. Phalangeal length estimates
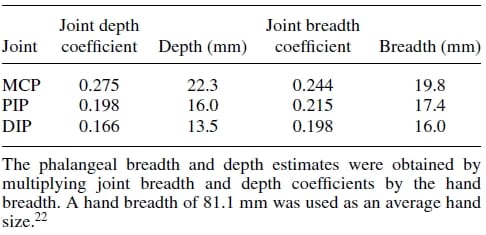
Table 3. Phalangeal depth and breadth estimates.
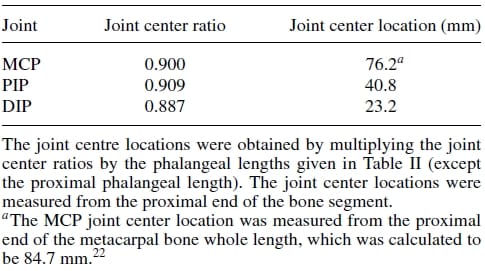
Table 4. Joint center location estimates.
3.2. Kinematically accurate motion
To enable a biological motion resemblance, the artificial finger was modeled after the natural hand’s kinematics. As shown in Fig. 3, our biomimetic artificial finger is hence made up of three links corresponding to the proximal, middle, and distal phalanges of the natural finger. Joint movement in the natural finger is described by the movement of the finger bone segments along articular surfaces. The convex and concave topologies of the contacting bone extremities characterize the human finger joint as ball-type joints. However, the finger joints are spanned by muscles, tendons, and ligaments which restrain the latter from having a 6 DOF motion. These kinematic constraints allow simplifications to be made when modeling the finger movement. Hence, the 2 DOF articulations at the MC Pare replicated using a universal joint, which mimics the biaxial nature of this joint. The PIP and DIP joints are modeled as hinge joints, since they are 1 DOF joits with articulation in the sagittal plane (plane perpendicular to the palmar surface) only. Buccholz et al.22 further suggested that an anatomical estimate of the joint center location can be defined at the head of the bone proximal to the given joint and that these joint centers remain fixed along the entire range of motion of the phalanges. Transferring these features to our model, fixed axes of rotation were implemented at the head of the proximal and middle phalanges for the PIP and DIP joints, respectively. In these joints, rotation occurs about a shaft common to the head of the proximal phalange and the base of the middle phalange for the PIP joint, and the head of the middle phalange and the base of the distal phalange for the DIP. A four-bar linkage mechanism mounted into the finger structure coordinates the PIP and DIP in flexion and extension replicating the natural motion of the two finger joints. In the natural finger, however, the lateral bands (which originate from the extensor hood) couple the DIP and PIP joints, enforcing their passive interdependence.

Fig. 2. CAD models for the proposed biomimetic artificial finger for the experimental testbed. (a) Nominal resting state. (b) Flexed state.
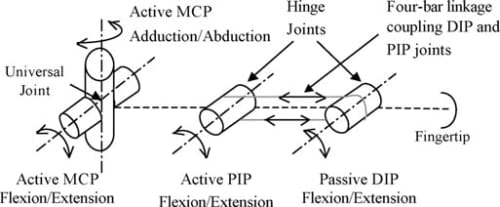
Fig. 3. Kinematic architecture of the artificial finger.
The ROM in the artificial finger joints reflect those of the natural index finger shown in Table I. A flexion/extension range of 90° and adduction/abduction of 40° is modeled at the MCP. Similarly, flexions/extensions of 100° at the PIP joint and 80° at the DIP joint are modeled. The flexion and extension limits of all joints are achieved by mechanical stops, incorporated within the structure of the links. In summary, Fig. 3 illustrates the kinematic architecture of the artificial finger.
A significant consideration in emulating the human finger is that, in its nominal resting position, the finger is not in a rigidly straight position along the palmar plane. The proximal phalange is at an angle to the palmar plane, while the finger segments are also at an angle to each other. Goniometric measurements of finger joint angles were subsequently performed on a test sample consisting of six subjects. Based on these measurements, it was determined that the proximal link’s resting position is at about 40° with respect to the palmar plane, while the middle link rests at an angle of about 20° with respect to the proximal link phalange. Figure 2(a) shows the nominal resting positions of the joints implemented in the artificial finger. In an extended position, however, the centers of rotation of the three joints lie in the same plane as the palmar plate (see Fig. 4). Note that in both resting and extended positions, the middle and distal links of the finger maintain a slightly bent (but at varying) position to each other, as they are connected at angles (using the internal four-bar linkage mechanism) to replicate the natural posture of the corresponding segments.
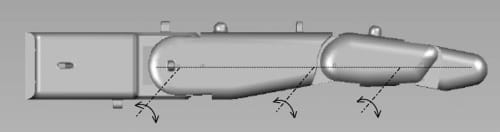
Fig. 4. Alignment of MCP, PIP, and DIP joints in the extended position.
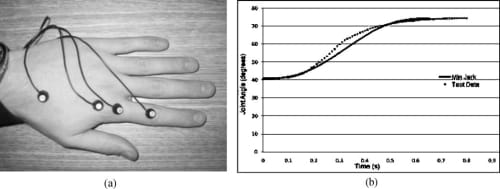
Fig. 5. Motion analysis on the MCP joint of the index finger to verify the minimum jerk model. (a) Placement of LEDs for Visualeyez system. (b) Comparison between the minimum jerk model and natural joint motion obtained using Visualeyez.
Minimum jerk approximation of natural finger motion. Jerk, which is the time derivative of acceleration, is a universally accepted quantity of evaluating motor smoothness of human limbs. If we apply Hogan’sminimum jerkmotor coordination theory24 to the motion of the natural finger joints, each joint should move smoothly from one position to another following a joint trajectory that minimizes the sum of the squared jerk, that is,
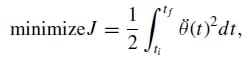
where θ(t) is the jerk of the joint trajectory θ(t). Hence, in order to create a truly biomechanically accurate artificial finger, its joint motion should follow a minimum jerk trajectory as well. The general solution to Eq. (1) is given by:

In order to verify the validity of the above minimum jerk joint trajectory model of the natural finger, a motion analysis was performed using a Visualeyez motion tracking system (from PheoniX Technologies Inc.). As shown in Fig. 5(a), four LED sensors were placed on a subject’s hand for the Visualeyz system, two on the metarcarpar bone and two on the proximal bone of the index finger. This setup allows the measurement of the MCP joint angle between the two bones, and the subject was asked to move the index finger from a nominal resting position to a flexed position at the MCP joint level. The dotted grey line in Fig. 5(b) is an average of 10MCP flexion trials, while the black line is the minimum jerk approximation over the same range of motion. It can be seen from the figure that the natural MCP flexion motion indeed follows a very similar trajectory to that of the minimum jerk model of Eq. (3). The model was found to be acceptable and was subsequently implemented as a biomimetic feedforward controller for the proposed artificial finger (Section 5.4).
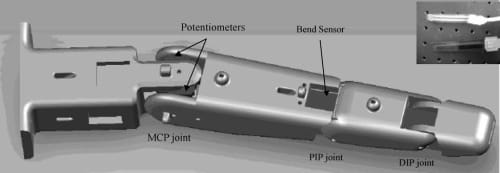
Fig. 6. A CAD representation of potentiometers and bend sensor embedded in the artificial finger. Contact force sensor is located at the fingertip (not shown). Inset shows the actual force (top) and bend (bottom) sensors.
3.3. Biomimetic sensory feedback
Resistive sensors, which offer a cost-effective solution for implementing sensory feedback in the artificial finger, use variable resistive characteristics of some conductive materials (e.g., conductive rubber, carbon, or polymer) to relay information about mechanical motions or forces. These sensors were chosen based on a number of factors— compactness, lightweight, good repeatability, and sensitivity and, of course, low price. As shown in Fig. 6, three different types of resistive sensors were chosen: thin-film flexible bend sensors, miniature rotary potentiometers, and thick-film flexible force sensors.
The commercially available flexible bend sensors (from Flexpoint Sensor System Inc.) consist of a thin polymide film coated with a carbon/polymer-based ink. When the film is bent, the micro separation of the coated ink changes the electrical resistance of the film. Among commercially available resistive bend sensors, Simone et al.25 suggested the Flexpoint bend sensors to be the most accurate and repeatable for measuring the natural finger flexion. For the present work, we chose a sensor with no polyester overlaminate, and mounted it within the upper inner layer of the artificial finger structure to act as internal proprioceptive sensors, providing positional feedback of the PIP flexion/extension movements. Note that the motions of the DIP and PIP joints are interconnected through the planar four-bar linkage mechanism; hence, given the position of the PIP joint, the position of the DIP joint can be easily determined.
While the bend sensors proved to be highly sensitive and reliable formonitoring the PIP flexion/extension movements, two miniature rotational potentiometers (Panasonic EVWAE4001B14) were employed for measuring the MCP flexion/extension and adduction/abduction movements, respectively. The 2 DOF motion requirement for the MCP joint prohibited the use of the bend sensors, as these can be allowed to bend only in one direction.
Although many different types of biomimetic tactile sensors have been proposed in the literature,26-28 it is still very difficult to replicate the multifaceted functionalities of the biological skin that is capable of multiple tactile sensing modes (see Section 2.3). In thiswork, only one tactile sensing mode—contact force—was attempted for practical reasons. The sensor is a commercially available polymeric thick-film force sensitive resistor (FSR) from Interlink Electronics. The force sensorwas applied only to the fingertip (proven sensory input location for finger dexterity) of the artificial finger, then covered it with a layer of elastomeric foam to evenly distribute any applied force and improve the repeatability of the measurements. Although this type of sensor is generally appropriate for qualitative rather than precision measurements, the performance was found to be sufficiently accurate for measuring fingertip forces (see Section 5.4).
4. Biomimetic Tendon-Driven Actuation Mechanism
4.1. Biomimetic tendon architecture
Human finger joint motion is produced by contracting muscles in the forearm and palm that are attached to the finger bones through a convoluted network of interdependently acting tendons and ligaments. The emulation of this complex architecture is, to date, an unattained benchmark. A partial physical modeling of the finger anatomy, namely the extensor mechanism, was achieved byWilkinson et al.29 However, the representation of this anatomical complexity is unnecessary for general rehabilitation robotic applications. In our work, large simplification of the complex tendon architecture is made possible due to the fact that we have mechanically represented the natural finger joints as simple 2 DOF universal (MCP) and 1 DOF hinge (PIP) joints. Hence, the multifunctionality nature of the natural tendons and ligaments that, as well as producing motion, also restricts the finger joint to 1 DOF or 2 DOF, was not fully replicated.
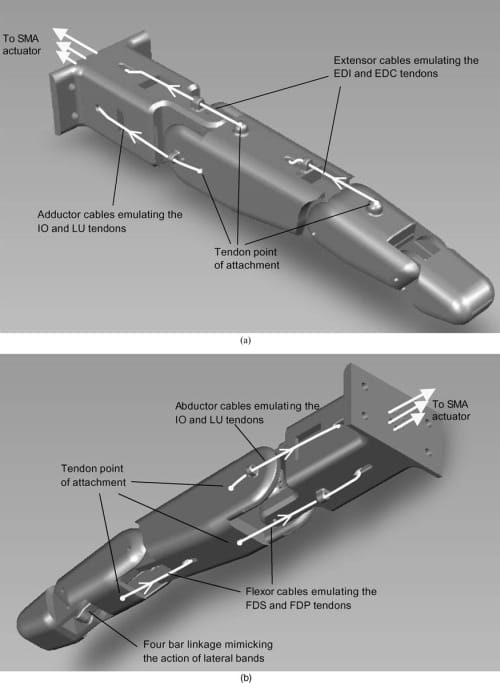
Fig. 7. (a) Extensor and adductor tendon cable configuration. (b) Flexor and abductor tendon cable configuration.
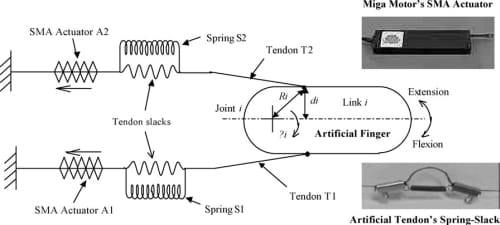
Fig. 8. Differential spring-biased SMA joint actuation mechanism. The insets show the actual SMA actuator and spring-slack element implemented.
4.2. Biomimetic actuation mechanism using compliant tendons and SMA artificial muscles
As shown in Fig. 7, flexible cables were attached directly to the artificial finger structure, mimicking the tendon-driven configuration of the natural finger. Two flexor cables were attached to the proximal and middle links emulating the FDS and FDP tendons. Two extensor cables were attached on the dorsal surface of the proximal and middle links, emulating the EDC and EI tendons. Finally, two adductor/abductor cables were connected to the ulnar and radial sides of the proximal joint mimicking the IO and LU tendons. The flexor, extensor, and adductor/abductor cables act as antagonist muscles enabling flexion/extension at the MCP and PIP and adduction/abduction at the MCP. As already mentioned, the DIP joint flexion/extension is coupled to that of the PIP joint by the implementation of the miniature four-bar linkage mechanism between those two joints inside the artificial finger structure. The four-bar linkage mimics the action of the natural finger’s lateral bands, coupling the PIP and DIP joints so that both joints attain their maximum flexion angles (100° at the PIP and 80° at the DIP) simultaneously. While the natural finger has no direct flexor and extensor attachment points to the proximal phalange (i.e., the MCP flexion/extension occurs through the action of the sliding extensor hood), the proposed tendon configuration allows the mimicking of the finger kinematics. Note that the exact attachment locations of the tendon cables on the finger structure were obtained in our previous work30 through kinematic and static torque analyses, which were omitted in this paper for the sake of brevity.
A spring-biased SMA mechanism is one where a spring is used to oppose the contraction of a SMA such that, when the wire cools, the spring’s opposing force helps the wire return to its original length. Typically, SMA-based robotic actuation systems, e.g., Elahinia and Ashrafiuon,31 consist of a single SMA spring-biased mechanism where link rotation is produced by the action of a one-way SMA actuator and the link’s return to the original position is made by a bias spring (either linear or torsional) connected in opposition to that actuator. However, when the human finger is in its natural resting position, it maintains a nominally flexed position (Fig. 2(a)). Full range of motion can be achieved by moving the finger in both flexion and extension directions about its nominal resting position. Since a spring-biased, one-way SMA actuation mechanism can only be used to pull the artificial finger in one direction (e.g. flexion or abduction) and not in the other direction (e.g., extension or adduction), we required an actuation mechanism that would permit biomimetic bi-directional (or differential) agonist–antagonist pulling motion about each finger joint. Furthermore, the elasticity of the natural muscle–tendons is a crucial characteristic of the finger’s kinematic architecture and needed to be replicated. In robotics, such compliance is a necessary element in providing stabilizing effect during contact tasks (e.g., gripping), especially in an unstructured environment.32
A schematic diagram of the proposed biomimetic compliant differential actuation mechanism is shown in Fig. 8. One end of the tendon cable is attached to the artificial finger structure, mimicking the attachment of the natural tendon to the finger bones, while the other end of the tendon cable is tied to the SMA actuator (from Miga Motors Company). The actuators are placed remotely to the finger joint, similar to the natural finger’s extrinsic musculature. Joint rotation is produced by the contractile action of two SMAactuators, placed in opposition to each other in a double spring-biased fashion. As shown in the lower inset of Fig. 8, passive compliance is introduced in the tendon cables of the artificial finger by connecting a spring in parallel to a slack portion of each tendon cable such that, as the SMA actuator contracts, the spring in the corresponding tendon elongates until the slack is absorbed and the tendon is taut. At this point, the tendon can be considered to have “infinite” stiffness and furtherSMAactuator contraction causes tension to be transferred to the finger for link rotation. This simple spring-slack artificial tendon effectively mimics the nonlinear stiffness of the natural tendon whose stiffness tends to infinity as it approaches its natural limit of extension. The dual spring-biased configuration permits the two SMA actuators to work as an agonist–antagonist pair, enabling both active extension and flexion of the joint.
In the proposed differential spring-biased actuation mechanism shown in Fig. 8, the spring S1 biases the SMA actuator A2, while the spring S2 biases the SMA actuator A1. Flexion occurs by the contraction of A1 on the finger while extension occurs by the contraction of A2. As an SMA actuator contracts, the spring in the tendon cable to which the actuator is connected to (we will refer this tendon as the “active tendon”) expands, absorbing the slack in the active tendon until the cable is fully stretched and taut. While the finger can rotate simultaneously during the absorbing of the slack (depending on the spring stiffness), at this point any further contraction of the SMA actuator acts directly on the finger along, rotating it about the joint axis. Simultaneously, as the finger flexes or extends, the spring in the opposing tendon (we will refer this tendon as the “passive tendon”) expands and the slack in the passive tendon is also absorbed.
Note that the springs in both the active and passive tendons need to be stretched whether the artificial finger is in a flexed or extended state with respect to its resting position. When an SMA actuator (A1 or A2) is deactivated and the contraction force is removed, the springs will go back to return to their original positions; and the spring in the active tendon recreates the slack. The spring in the opposing passive tendon reverse-biases the SMA actuator, exerting a pulling force on the artificial finger structure, and returns the joint to its original position. While the nonlinear stiffness property of the biological tendons limits the flexion/extension range of the natural finger, the limit on the range of motion of the artificial finger is dependent on the following two factors: (i) SMA actuator’s contraction range—the SMA actuator’s stroke range must be sufficiently large to first absorb the slack in the active tendon to which it is connected in order to produce joint rotation, and (ii) slack length in the passive tendon opposing the motion—the link cannot rotate beyond the elastic limit of the opposing tendon. As such, the proposed actuation mechanism demands a careful balance between the allowable tendon slack and the SMA contraction range to generate the desired range of motion.

One of the practical limitations of the chosen differential SMA actuation configuration is that, due to the presence of the slacks in the tendons, only a portion of the SMA strain ranges are available to cause the effective joint rotation. However, because of the fact that two SMA actuators are employed for active bi-directional rotation of each joint DOF, its overall range of motion is still greater than that of an equivalent single spring-biased SMA actuation mechanism (with no slack). Furthermore, the combined action of the spring and SMA in the tendon cable mimics the characteristics of the natural muscle–tendon, providing power only during contraction, yet providing compliance to deal with an opposing load as well. Also note that SMA actuators can be controlled in partial contraction, allowing finger links to be partially flexed and extended. The use of the two opposing SMA actuators per DOF allows the additional benefit of more precise finger positioning, as the direction of motion can be quickly reversed at any point during joint rotation.
Dynamic modeling and control design of the proposed actuation system will be addressed in Part II of this work.
5. Experimental Evaluation
5.1. Experimental setup
The experimental setup consisted of a biomimetic artificial finger, which was constructed using a Stereolithography rapid prototyping system (SLA-3500),mounted on an optical breadboard (see Fig. 9). The SMA actuators (DM01-15- PULL), which are off-the-shelf products from Miga Motor Company, were mounted on the breadboard as well. The patented internal architecture of MigaMotor’s SMA actuator produces a relatively large stroke length in a compact, lightweight housing. It is capable of producing a half inch linear stroke with a maximum contracting force of 20 N. In addition to providing a mounting surface, the aluminum breadboard also acted as a heat sink, improving the cooling rate of the actuators (however, this advantage would not be available in a real prosthesis/orthosis). The artificial tendon cables were attached to the finger structure, routed through the finger core and connected to their corresponding SMA actuators. A Teflon-coated microfibre line (SpiderWire’s Stealth) was chosen for the tendon cables. This allowed the creation of strong tendons that were also resistant to twisting and abrasions, so that they could easily be routed and fitted within the finger structure, without risking failure through frictional contacts or sharp bends. More importantly, the material’s teflon coating provided a very low coefficient of friction—an important consideration where the tendons had to pass through several guides and traveled in directions at various angles.
A microcontroller (PIC16F917) from Microchip Technologies was used to control the finger motion. For preliminary evaluation purposes, the microcontroller was programmed with a simple ad hoc proportional derivative (PD) controller as described in Section 5.3 and generated a pulse-widthmodulation (PWM) control signal based on a set reference value (which can be a desired joint positional angle or fingertip force) entered by the user. The PWM control signal operated power MOSFET transistors, acting as switches to modulate the voltage applied to the SMA actuators. The microcontroller’s built-in analog-to-digital (A/D) converter translated analog feedback information from the finger sensors to a digital form suitable for handling by the microcontroller. Serial configuration data sent by a host PC (through an RS232 port) were processed by the microcontroller’s built-in UART that performed serial to parallel and parallel to serial data conversion to and from the microcontroller.
A terminal program running on the host PC was used for communication with the finger’s microcontroller. The user interface was based on a menu structure with all text prompts generated by the microcontroller’s firmware.Once all control gains and desired final finger positions (or a fingertip force) were entered, the finger was capable of operation as a standalone device. The microcontroller’s firmware sampled the position of the finger in space by reading the appropriate sensors at 100 Hz, and generated appropriate closed-loop PWMcontrol signals until the desired finger position or force value was reached.

Fig. 9. Artificial finger testbed with six tendon cables routing through the finger core and attached to the corresponding six remotely placed SMA actuators. (a) Artificial finger prototype constructed using SLA-3500 RP machine loaded with Vantico CibaTool SL5510 resin. (b) Artificial finger and six SMAs mounted on optical breadboard.
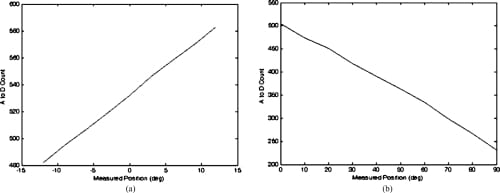
Fig. 10. Sensor response plots for the MCP abduction/adduction and MCP flexion/extension potentiometers. (a) MCP abduction/adduction potentiometer calibration curve. (b) MCP flexion/extension potentiometer calibration curve.
5.2. Sensor calibration
To provide valid experimental results, it was necessary to calibrate the various angle sensors and fingertip force sensor employed in the system. For all sensors used, calibration was done in terms of the number of A/D counts reported by the microcontroller’s built-in A/D converter. Calibration of the various joint angle sensors was performed using a goniometer designed for human finger joint angle measurement. Calibration of the fingertip force sensor was performed by static loading of the sensor using a series of weights of known mass and a load cell.
The rotary potentiometer selected for the measurement of the MCP flexion/extension and MCP adduction/abduction is an inherently linear device and, beyond simply correlating joint angles with the resulting A/D count values and applying a basic straight line fit, no further manipulation of the data was required. The resistive bend sensor used for the PIP flexion/extension measurements and the resistive force sensor used for measuring the fingertip forces are, however, nonlinear in their responses. It was found that the embedded control algorithms were sufficiently robust that the linearization of the output from these sensors was unnecessary. However, it was necessary to plot the sensor’s response and find a fourth-order polynomial fit to the response curves to facilitate the creation of a look-up table for the microcontroller. Figures 10 and 11 showthe responses obtained from the various sensors.
5.3. Control strategy
SMAs are inherently nonlinear and hysteretic in nature and, as such, pose a challenge as far as the implementation of an accurate and robust controller is concerned. Furthermore, the dynamic behavior of SMAs is highly dependent on the fabrication process, alloy content, and training. High parametric uncertainty accompanies the nonlinear SMA models31,33 available in the literature, further complicating the design of a controller. A robust controller is required in order to account for all nonlinearities and allow precise control of the proposed spring-biased differential SMA actuation system—this will be addressed in Part II of this work. In this paper, the focus was placed on quick testing and evaluation of the actuation mechanism with a simple and practical embedded pulse-width-modulated proportional-derivative (PWM-PD) controller.
During SMA actuation, the martensitic and austentic transformation rates of the SMA wire are controlled solely by the rate at which heat is transferred to and removed from the wire. In the case of electrical (or joule) heating, heat transfer is dictated by the level of current applied. While electrical heating using direct current (DC) is very effective in rapidly increasing the material’s temperature, merely turning the current off once the desired actuator position is reached is not a solution, since the actuators return to their initial extended position upon cooling. Therefore, a means of varying the amount of heating power supplied to the actuator SMA wire is required. Direct control of the actuator’s DC voltage would be one way to vary the amount of heating that the SMA wire experiences, and therefore the degree to which a state change progresses. Direct control is, however, wasteful of energy, with whatever fraction of the power not required by the actuator load being simply dissipated as waste heat. PWM is a more practical approach, where the relatively slow response time of an SMA element serves to average the duty cycle of PWM signals, enabling uniform heating and effective control over the transformation process.33 Little heat is generated with this method of control and rechargeable batteries can be used to provide power to theSMAactuators in stand-alone, ambulatory applications in rehabilitation robotics. In addition, PWM has the advantage of being easily implemented using microcontrollers.
Hence, PWM voltage signals were used as the control variable and integrated with a PD feedback controller possessing a satisfactory stability margin for standalone operation of the biomimetic artificial finger. The required controller was implemented completely in firmware programmed into the system’s microcontroller. In addition, an integral feedback term was also calculated although not used in this Part I of the work. However, the end result was a microcontroller-based system capable of controlling finger joint motion under fully embedded PWM-PID control, and the proportional (Kp), integral (Ki), and derivative (Kd) gain terms were all user-programmable.
The PWM signals applied are voltage signals of uniform height and variable duration. Varying the duty cycle of the PWMsignal varies the average control energy that is directed to the SMA actuator. Increasing the duty cycle increases the applied energy, causing the temperature of the actuator to increase, thus increasing the rate of actuator contraction. If the duty cycle is reduced below the actuation threshold, the wire cools below the actuation temperature, and a reverse bias force will then cause the SMA wire to stretch toward its original prestrained length. If the duty cycle is, on the other hand, maintained at just the threshold actuation value, the SMA wire maintains its existing length without any change in strain. The actuator contraction rate is, thereby, controlled by varying the duty cycle of the applied voltage until the desired angular position is achieved. Note that the maximum applicable voltage is 28 V for the chosen Miga Motor’s SMA actuator. However, this voltage level reduces the SMA actuator life and may cause overheating. As such, a voltage level of 8 V was chosen for the PWM signal, since this voltage level yields adequate actuator response without compromising actuator life. A constant PWM frequency of 225 Hz was used with the duty cycle capable of being varied from 0 to 100%. Experimental identification showed that a minimum 20% threshold duty cycle was required to maintain the SMA actuator in a steady activated state.
The set point for the controller is a desired angular position (θd) (or desired fingertip force for closed-loop force control). The positional sensors (the bend sensor and potentiometers) measure the actual angular position (or the force sensor measures fingertip force), which is fed back to the controller. The error signal, which is the difference between the desired and measured values, is fed into the controller and a proportional error term and a derivative error term are calculated. The proportional and derivative error terms are then added to produce the final control signal. The resulting value is then scaled to provide a corresponding PWM signal with a value somewhere between 0 and 100% duty cycle.
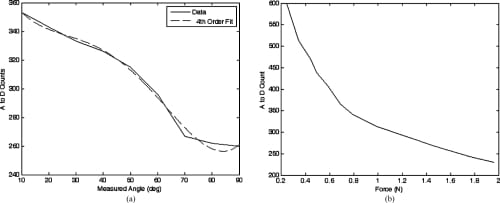
Fig. 11. Sensor response plots for the PIP bend sensor and fingertip force sensor. (a) PIP flexion/extension bend sensor calibration curve with a fourth order polynomial fit. (b) Fingertip force sensor calibration curve.
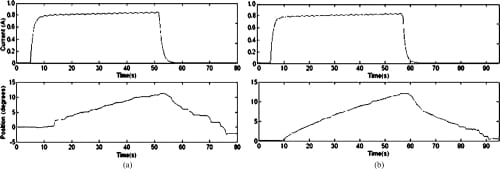
Fig. 12. Open-loop MCP adduction and abduction motion profiles. (a) MCP adduction: open loop. (b) MCP abduction: open loop.
5.4. Experimental results
The controller gains (Kp and Kd) used in this paper are obtained and tuned using direct experimental observations rather than a complex nonlinear mathematical model of the system, which will be derived in Part II. The resulting gain values varied depending on the particular joint DOF being activated and the direction of actuation (e.g., flexion versus extension), ranging typically from 500 to 10,000. It was found that the response time of the controller, which had an update rate of 10 ms, and large gain values were possible without instability or overshoot problems.
The purpose of the following experimentswas to demonstrate the 3 DOF active motion (excluding the 4th passive DOF) of the biomimetic artificial finger via the proposed springbiased differential SMA-based tendon-driven actuation system. Open-loop tests were first performed to assess the effectiveness of the actuation mechanism designed, most specifically with respect to the agonist–antagonist motion of each active finger joint. Closed-loop tests were then carried out to assess the performance of incorporating feedback control into the system.
As shown in Fig. 9(a), the artificial finger was placed in the nominal resting position to mimic the natural posture of the human finger when at rest. The springs and the slacks in the tendons were adjusted under slight tension to always maintain the finger in this initial position when the SMA actuators are inactive. The MCP joint was thus positioned at 40° to the metacarpal link and the PIP joint at 20° relative to the proximal link. The passive DIP was automatically positioned by the four-bar linkage coordinating the PIP and DIP joint motion. Joint motion was initiated by a user request to move the link into a desired position. The controller generated a PWM signal of fixed duty cycle for open-loop motions and variable duty cycle for closed-loop motions. The open-loop duty cycle was limited to 50% to avoid overheating of the SMAwires inside the actuator, and hence permanent damage.
Given the points of attachment of the elastic tendons from the finger’s joint centers and the slack required in each tendon, the required minimum SMA contraction length was calculated to be at least 1 inch as per Eq. (8). However, although the tendon slacks were set up to enable full ranges of joint motion (i.e., 50° flexion, -40° extension, and +/-20° adduction/abduction at the MCP; 80° flexion and -20° extension at the PIP joint about the resting position), the actual range of motion tested was restricted due to the limited stroke of the Miga Motor’s SMA actuators that we employed (i.e., 0.5 inch; 1 inch stroke SMAactuators are being custombuilt as our ongoing work). Our preliminary experimental testing showed that only the following joint ranges could be obtained repeatedly in the closed-loop configuration without damaging the SMA actuators: MCP adduction/abduction of +/-15°,MCP flexion/extension of +/-20°, and PIP flexion of +25° and extension of -15° about the resting position.
Since SMA contraction responds to temperature changes caused by joule heating, the average current delivered to the SMA wire was measured. Open-loop tests showed that an average of about 0.7 to 0.8 A was sufficient to produce joint motion. This was achieved by setting the PWM to a 50% duty cycle. The open-loop graphs (Figs. 12–14) indicate satisfactory but slow (at certain joints) agonist–antagonist motion of the finger link. For instance, the rate of motion for MCP abduction/adduction as well as MCP flexion/extension was much slower than that for PIP flexion/extension. The relatively high joint settling times at the MCP are related to the high torques required to move the entire finger structure at that joint, while at the PIP, the SMA actuator acts on the middle and distal links only. The double spring-biased mechanism successfully returned each joint to its original position. However, the return process was slow and unsteady in all open-loop cases, with an unacceptable return period in the 20- to 30-s range. This behavior is due to the high cooling times associated with the Miga Motor SMA actuators that prevent their fast return. Furthermore, once actuator power was applied, a time delay of approximately 2–8 s (depending on duty cycle) was observed before joint motion occurred. This delay corresponds to the SMA actuation time (about 1 s at a constant 8 VDC), as well as the time required for some initial slack to be absorbed from the tendon cables before the actuator affects joint motion.
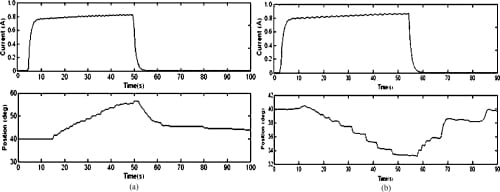
Fig. 13. Open-loop MCP flexion and extension motion profiles. (a) MCP flexion: open loop. (b) MCP extension: open loop.
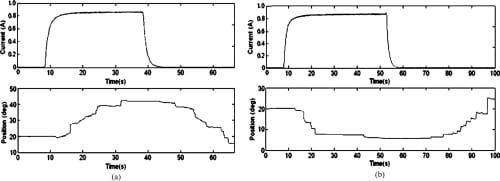
Fig. 14. Open-loop PIP flexion and extension motion profiles. (a) PIP flexion: open loop. (b) PIP extension: open loop.
The closed-loop plots (Figs. 15–17) showed that the feedback control incorporated into the system significantly improved the performance of the joint motion of the finger. The controller produced signals of variable duty cycle based on the current link’s position (as measured by the bend sensors) with respect to the desired position. The current graphs indicate a sharp increase in the current level to a peak value of approximately 1.4 to 1.5 A at the beginning of the joint motion. The current then tapered to a lower level as the desired joint angle was approached. Finally, the current reduced to a still lower value sufficient to hold the finger in position once the desired joint angle was reached. This current profile behavior suggests that aPWMsignal with high duty cycle was initially generated, enabling the SMA wire to heat up rapidly. The PWM duty cycle was then reduced to a value yielding a constant actuator position that corresponds to a desired joint position.
The embedded PWM-PD controller was highly effective in reducing the response time of the system, enabling final positions to be achieved within a matter of seconds. Once the desired angular position was achieved, the finger maintained a steady posture. Although the closed-loop position control produced rapid and steady finger motion, spring-biased return to the original resting position was observed to be still slow in the closed-loop configuration as well, which is expected, since the return to a neutral position was effected simply by removing actuator power, as in the open-loop case. Powering the opposing actuator during the joint’s return phase to its resting position would be an obvious solution to this problem, which will be addressed in Part II. Also, adding some sort of an active heat sink to the SMA actuator should increase the SMA cooling rate and improve the rate at which the finger joints return to their resting position.
Next, the biomimetic feedforward controller (i.e., the minimum jerk trajectory) that was developed in Section 3.2 was added to the PWM-PD feedback controller of the artificial finger. The minimum jerk path was calculated for the range of motion of the finger at the MCP (from relaxed to flexed) and was implemented as a look-up table in the microcontroller. The artificial finger was driven to follow the lookup table and its resulting motion was analyzed using the Visualeyez system, which showed a satisfactory agreement between the actual motion and the minimum jerk reference motion (Fig. 18).
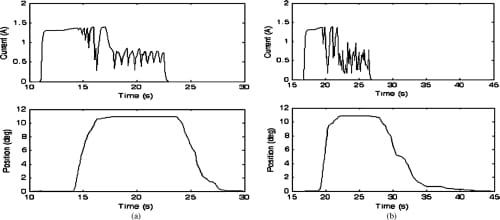
Fig. 15. Closed-loop MCP adduction and abduction motion profiles and the current profiles of the corresponding SMA actuators. Starting from a nominal position of 0°, the set values of 11° for both adduction and abduction were successfully achieved. (a) MCP adduction: closed loop. (b) MCP abduction: closed loop.
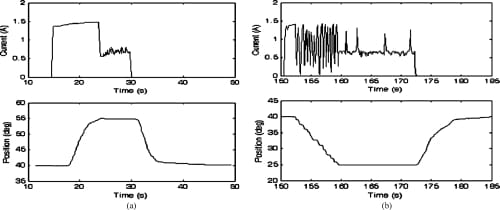
Fig. 16. Closed-loop MCP flexion and extension motion profiles and the current profiles of the corresponding SMA actuators. Starting from a nominal position of 40°, the set values of 55° and 25° for flexion and extension, respectively, were successfully achieved. (a) MCP flexion: closed loop. (b) MCP extension: closed loop.
One of the main functional tasks of the human hand is the grasping of objects, and the amount of force applied while holding an object must be precisely controlled. Therefore, once the ability to move finger joints to set positions had been evaluated, a subsequent experiment was performed to ascertain howsuccessfully closed-loop force control could be applied to the fingertip. It was decided that closed-loop force control of the PIP joint would be the most logical approach, since that joint is directly linked to the fingertip’s DIP joint. The fingerwas oriented to allowthe fingertip pressure sensor, mounted near the end of the underside of the DIP joint, to transfer force to a load cell for force measurement. A desired fingertip force (an A/D count value corresponding to approximately 0.2 N force) was input to the controller and the PIP flexion actuator began applying force that was transferred to the load cell and the fingertip force sensor. The results of this experiment are shown in Fig. 19.
Due to the particular circuit configuration for this force sensor, decreasing A/D count readings correspond to increasing force values. It can be seen that the finger reaches a steady-state value where approximately the desired fingertip force is applied to the load cell. However, one potential issue of consequence can be seen in looking at the plot: over time, the actual measured fingertip force decreases while the force reported by the fingertip force sensor stays relatively constant. This is due to the type of sensor (i.e., FSR) chosen to measure the fingertip force. When compressed for long periods of time (more than a few seconds) the resistance of the thick-film sensor slowly changes. All sensors of this type exhibit this shift to a degree, with some manufacturer’s sensors being better than others in this regard. However, this effect is reversible once pressure is removed from the sensor. The low cost and lightweight advantages of this type of sensor made its use attractive for the artificial finger, and incorporation into rehabilitation robots might still be practical given the relatively small magnitude of the phenomenon, and the fact that the human hand is not generally required to grasp objects for long periods of time with significant accuracy.
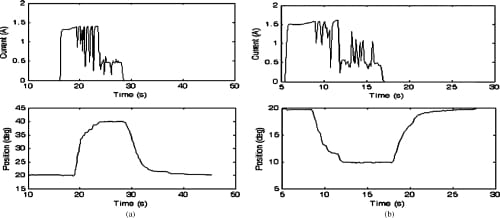
Fig. 17. Closed-loop PIP flexion and extension motion profiles and the current profiles of the corresponding SMA actuators. Starting from a nominal position of 20°, the set values of 40° and 10° for flexion and extension, respectively, were successfully achieved. (a) PIP flexion: closed loop. (b) PIP extension: closed loop.
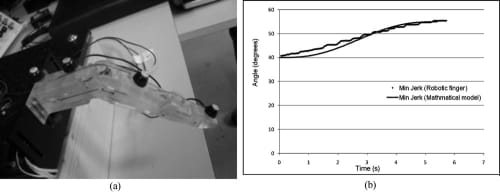
Fig. 18. Comparison between reference and actual minimum jerk flexion trajectories of artificial finger’s MCP using Visualeyez motion tracking system. (a) Placement of LEDs for Visualeyez system. (b) Closed-loop MCP joint following minimum jerk flexion trajectory.
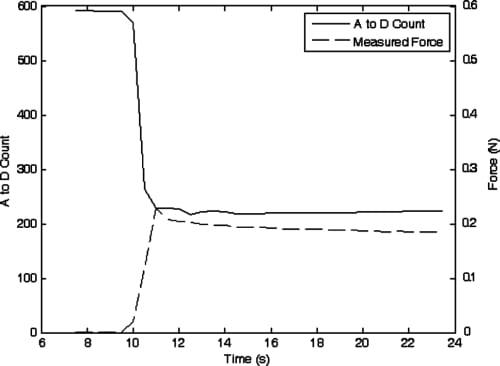
Fig. 19. Sensor A to D counts and measured fingertip force while attempting to apply 0.2 N force using PIP joint force control.
6. Conclusion
The aim of this work was to emulate the biological features of the natural muscle–tendon arrangement in the human hand in developing a new actuation mechanism for a biomimetic artificial finger. It is based on the integration of compliant tendon cables and one-way shape memory alloy (SMA) wires in an agonist–antagonist artificial muscle pair configuration for the required flexion/extension or abduction/adduction of the finger joints. An anthropomorphically and biomechanically accurate artificial finger was also developed as a platform to test the proposed actuation mechanism. The main features of the proposed biomimetic actuation and finger system can be summarized as: (i) anthropomorphically accurate size and appearance; (ii) kinematically accurate joint motion, (iii) compliant and tendon-driven muscle-like actuation, and (iv) biomimetic sensory feedback. The entire system is a compact, low-cost, lightweight, stand-alone system suitable for ambulatory applications (e.g., prosthetic and wearable robotics) in rehabilitation robotics, while capable of producing similar manipulative and functional abilities found in the natural finger. A microcontroller-based pulse-width-modulated proportional-derivation (PWMPD) feedback controller and a minimum jerk trajectory feedforward controller were implemented in an ad hoc fashion to evaluate the performance of the finger system in producing closed-loop biomimetic joint motions.
References
- H. H. Kwee, “Rehabilitation robotics—Softening the hardware,” IEEE Eng. Med. Biol.Mag. 14(3), 330–335 (1995).
- G. Bolmsjo, H. Neveryd and H. Eftring, “Robotics in rehabilitation,” IEEE Trans. Rehabil. Eng. 3(1), 77–83 (1995).
- N. Tejima, “Rehabilitation robotics: A review,” Adv. Robot. 14(7), 551–564 (2000).
- D. Stefanov and Z. Z. Bien, “Advances in human-friendly robotic technologies for movement assistance/movement restoration for people with disabilities,” In: Advances in Rehabilitation Robotics (Z. Z. Bien and D. Stefanov, eds.) (Springer, Berlin, 2004) pp. 3–23.
- D. Popovic and T. Sinkjar, Control of Movement for the Physically Disabled (Springer, London, 2000).
- H. Herr, G. Whiteley and D. Childress, “Cyborg technology – Biomimetic orthotic and prosthetic technology,” In: Biologically Inspired Intelligent Robots (Y. Bar-Cohen and C. Breazeal, eds.) (SPIE Press, Bellingham, WA, 2003).
- Z. Li and S. Sastry, Dexterous Robot Hands (Springer, New York, 1989).
- J. L. Pons, R. Ceres and F. Pfeiffer, “Multifingered dexterous robotic hand design and control: A review,” Robotica 17, 661– 674 (1999).
- L. Lin and H. Huang, “NTU hand: A new design of dexterous hands,” Trans. ASME, J. Mech. Des. 120, 282–292 (1998).
- H. Liu, P. Meusel, J. Butterfass and G. Hirzinger, “DLR’s multisensory articulated hand, part II: The parallel torque/position control system,” Proceedings of the IEEE International Conference on Robotics and Automation, Leuven, Belgium (1998) pp. 2087–2093.
- C. S. Lovchik and M. A. Diftler, “The robotnaut hand: The dexterous robot hand for space,” Proceedings of the IEEE International Conference on Robotics and Automation,Detroit, MI (1999) pp. 907–912.
- M. C. Carrozza, B. Massa, P. Dario, M. Zecca, S. Micera and P. Pastacalsi, “A two DOF finger for a biomechatronic artificial hand,” Technol. Health Care 10, 77–89 (2002).
- C. Liang and C. A. Rogers, “Design of shape memory alloy actuator,” Trans. ASME, J. Mech. Des. 114, 223–230 (1992).
- P. J. Kyberd, C. Light, P. H. Chappell, J. M. Nightingale, D. Whatley and M. Evans, “The design of anthropomorphic prosthetic hands: A study of the southampton hand,” Robotica 19, 593–600 (2001).
- C. P. Chou, “Measurement and modeling of McKibbon pneumatic artificial muscles,” IEEE Trans. Robot. Autom. 12, 90–103 (1996).
- F. El Feninat, G. Laroche, M. Fiset and D. Mantovani, “Shape memory materials for biomedical applications,” Adv. Eng. Mater. 4, 91–104 (2002).
- N. Yoshiyuki, “Hitachi’s robot hand,” Robot. Age 6(7), 18–20 (1984).
- K. J. De Laurentis and C. Mavroidis, “Mechanical design of a shapememory alloy actuated prosthetic hand,” Technol.Health Care 10, 91–106 (2002).
- A. D. Price, A. Jnifene and H. E. Naguib, “Design and control of a shape memory alloy based dexterous robot hand,” Smart Mater. Struct. 16, 1401–1414 (2007).
- B. Tyldesley and J. I. Grieve, Muscles, Nerves and Movement: Kinesiology in Daily Living (Alden Press, Oxford, 1989).
- G. M.Wybrun, R.W. Pickford, R. J. Hirst, Human Senses and Perception (Oliver and Boyd, London, 1969).
- B. Buchholz, A. Armstrong and S. A. Goldstein, “Anthropometric data for describing the kinematics of the human hand,” Ergonomics 35(3), 261–273 (1992).
- P. K. Levangie and C. C. Norkin, Joint Structure and Function: A Comprehensive Analysis, 3rd ed. (F.A. David Company, Philadelphia, PA, 1992).
- N. Hogan, “An organizing principle for a class of voluntary movements,” J. Neurosci. 4, 2745–2754 (1984).
- L. K. Simone and D. G. Kamper, “Design considerations for a wearable monitor to measure finger posture,” J. NeuroEng. Rehabil. 2(5), 1–10 (2005).
- D. J. Beebe, D. D. Denton, R. G. Radwin and J. G.Webster, “A silicon-based tactile sensor for finger-mounted applications,” IEEE Trans. Biomed. Eng. 45(2), 151–159 (1998).
- J. Engel, J. Chen, Z. Fan and C. Liu, “Polymer micromachined multimodal tactile sensors,” Sensors Actuators A 117, 50–61 (2005).
- J. Carpaneto, S. Micera, F. Zaccone, F. Vecchi and P. Dario, “A sensorized thumb for force closed-loop control of hand neuroprostheses,” IEEE Trans. Neural Syst. Rehabil. Eng.
11(4), 346–353 (2003). - D.Wilkinson, M.VandeWeghe andY. Matsuoka, “An extensor mechanism for an anatomical robotic hand,” Proceedings of the IEEE International Conference on Robotics and Automation,
Taipei, Taiwan (2003) pp. 238–243. - V. Bundhoo and E. J. Park, “Design of an artificial muscle actuated finger towards biomimetic prosthetic hands,” Proceedings of the IEEE International Conference on Advanced Robotics, Seattle, WA (2005) pp. 368–375.
- M. Elahania and H. Ashrafoun, “Nonlinear control of a shape memory alloy actuated manipulator,” Trans. ASME. J. Vib. Acoust. 124, 566–575 (2002).
- J. I. Arocena and R.W. Daniel, “Design and control of a novel 3-DOF flexible robot, part 1: Design and evaluation,” Int. J. Robot. Res. 17, 1167–1181 (1998).
- N. Ma and G. Song, “Control of shape memory actuator using pulse width modulation,” Smart Mater. Struct. 12, 712–719 (2003).